Part 1: Introduction to CalcArrays
Prelude
The 2048 Power Compendium is a collection
of 100 different gameplay variants of 2048, most of which were made by me (but some came from elsewhere or were
suggested by players, though as of them they were all still coded, or at least re-implemented, by me).
Several of the people on my Discord server have taken an interest
in working with the code of the game
(which is open-source and can be found on GitHub),
so I figured I'd write a detailed explanation of how it works to aid them.
This blog post assumes you have some programming knowledge - the 2048 Power Compendium is coded in JavaScript,
though by the nature of programming languages, if you know some other programming language you'll probably still
be able to read this, seeing as JavaScript itself isn't what this post is about per se.
On the surface, the 2048 Power Compendium appears to be a collection of 2048 variants, but
internally it's more like an engine for loading and running 2048 variants,
which has 100 of them set to be loaded already. The code for loading a variant looks like this:
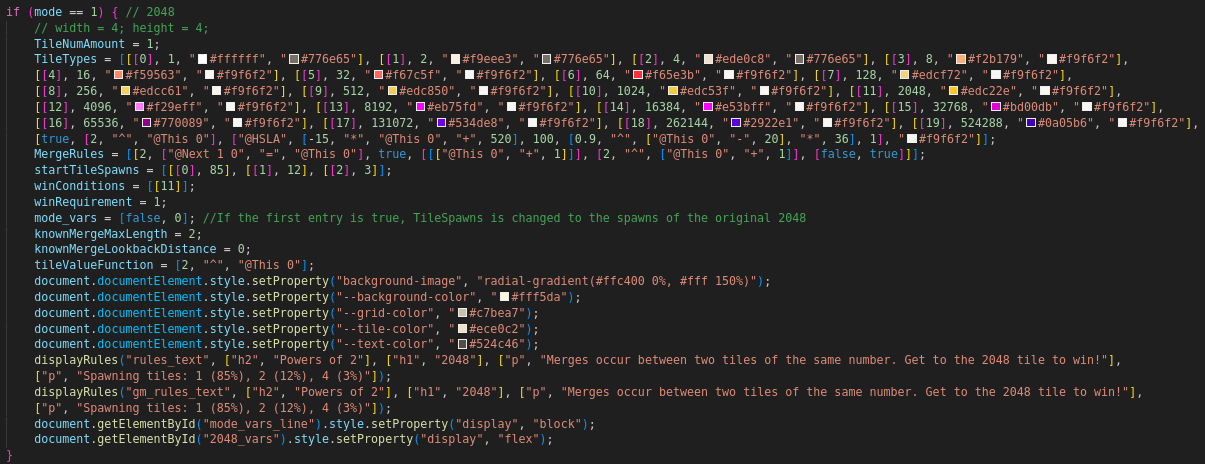
If the variants were being run directly in JavaScript, you'd expect something like
if {Grid[y][x] == Grid[y][x + 1]} somewhere in there to check
whether two tiles are equal. But instead of a bunch of if statements, there's a bunch of arrays.
MergeRules and the last entry of TileTypes seem especially curious - what's up with "@This 0"
and those mathematical expressions written as arrays?
That is what this blog post will explain.
(Before we begin, here's a warning: there are secrets hidden in the 2048 Power Compendium,
and this blog post will give some spoilers for a couple of them. If you wish to find those
secrets yourself, I recommend waiting to read this blog post until you do.
If you do not know yet whether you have found all of the secrets, then you have not.)
What is a CalcArray?
The code that the 2048 Power Compendium runs to do things like merges is not written directly
in JavaScript. It's written in CalcArrays, a sort of programming language
within the Power Compendium's code.
In their most basic form, CalcArrays evaluate simple math operations.
For example, [4, "+", 5] will evaluate to 9.
If you're using the JS console on the Power Compendium website and wish to try out CalcArrays as we go,
use the function CalcArray(); for example,
CalcArray([4, "+", 5]); will return 9.
CalcArrays have no concept of an order of operations, they simply evaluate from left to right.
For example, when evaluating [3, "+", 2, "*", 4], the addition is done first
since it comes first in the array, so that array simplifies to [5, "*", 4],
which returns 20.
There is, however, an equivalent to parentheses: nested arrays. An array inside a CalcArray will itself
be evaluated as a CalcArray, so [3, "+", [2, "*", 4]] becomes
[3, "+", 8], which returns 11.
Generally, when using an operator, the order of the arguments is
argument 1, operator, argument 2,
where often argument 1 is the result of everything up to that point.
If an operator only has one argument, then it's just argument 1, operator.
If an operator has more than two arguments, it's argument 1, operator, argument 2, argument 3, argument 4...
up until the last one. All operators, with the exception of some special things that are moreso control tools than operators,
have a fixed number of arguments.
CalcArrays can do a lot more than basic arithmetic, and numbers aren't the only data types that CalcArrays work with.
They can also work with a few other types,
such as strings, booleans, and bigints. Type conversion is automatic: each operator
has a type it works with (with a few exceptions), and when it's time to apply that operator,
its arguments will be automatically converted to that type before it's applied.
CalcArrays can also do things like
loops, conditionals, variables, and so on. We'll be going over all of those throughout this blog post.
Where and Why are CalcArrays used?
CalcArrays are used in a few places when creating a mode in the Power Compendium:
-
They're used to define how tiles are displayed, including checking whether a tile matches a certain pattern,
and defining the colors of tiles.
-
They're used in several places in merge rules: to define the condition that has to be true for tiles to merge,
to express the output tile(s) in terms of the input tile(s), to define what the score is changed by based on the input tiles,
and some other things for particular merge rules.
-
In modes where the spawning tiles, the win conditions, etc. are more complicated than just an unchanging list,
CalcArrays are used to express them.
-
Finally, some modes have additional "scripts" they run at certain times: for example,
mod 27 has a script to change the modulus when a 1 is made, and DIVE has a script for adding and removing seeds at the end of a turn.
These scripts are written using CalcArrays.
But why does the Power Compendium have a custom "programming language" for all these
instead of just writing them in JavaScript? There are two main reasons:
-
First, it makes modes easier to make for me, MathCookie17, the developer of the Power Compendium.
More complicated modes like DIVE are harder to make in CalcArrays than in JavaScript, but for the easier modes
(basically any mode on the first two pages, and many on page 3), CalcArrays make it easier,
since they were designed to make writing merge rules easy. Rather than having to write JS code for checking
every merge type in each direction for each mode, I can just write a couple CalcArray merge rules and let
the "engine" handle the JavaScript checks for me. This allows me to make a Page 1 or Page 2 style mode
in significantly less than an hour - and most of that time is spent choosing colors for the tiles anyway.
-
Second, it's the reason save code support works.
A 2048 Power Compendium save code does not just contain a number indicating what mode it's loading into.
Instead, the save code contains the rules and all of the mode itself in addition to your round's current state.
This means you could theoretically load a save code into a version of the Power Compendium that didn't contain that mode,
and the mode would still load fine. In practice, each major version of the Power Compendium adds new features to CalcArrays,
or at least new special color schemes, that mean it wouldn't be guaranteed safe to load a save code from it into a previous version,
so the game doesn't let you, but that's besides the point.
What the save codes do let you do is, in theory, export your own modes: if you learn how to use the Compendium's code
yourself and create a mode in it, you can save that mode as a save code and share it with others, who can play it even if they
don't know how to modify the Compendium themselves, simply by loading in the save code (such modes have been dubbed "injected modes"
by my Discord server).
If the definitions of modes were written in JavaScript,
the save codes would have to export JavaScript code as a string, and then turn it into functions via
eval() or the like. This, as any JavaScript developer probably knows, is a major risk -
save codes would be much more likely to break (or be created maliciously!) in ways that could do harmful things to your computer.
Having all the "code" of a mode be written in an array format rather than as real code makes it a lot easier
to save it as a string, and also safer, since in theory CalcArrays can't escape their scope and affect things outside
the things in the Compendium they're allowed to affect (they could, of course, be used to crash the Compendium with a simple
infinite loop, but they shouldn't be able to do more harm than that).
We'll get to how to use CalcArrays in these places later on, but first we need to discuss how to use them on their own,
because even when they're not attached to a tile type, merge rule, or other such structure, they can still be
used as a programming language of sorts - at least in the console, anyway.
Part 2: CalcArray Operators
Number Operators
Let's start with the operators for numbers, since those were what CalcArrays were originally designed to work with.
Here's a list of the operators that are generally used with numbers.
Unless otherwise stated, the arguments to these operators are numbers, and the value they result in is a number.
-
"+" (2 arguments): Addition. Result is the sum of the two numbers.
-
"-" (2 arguments): Subtraction. Result is the difference of the two numbers.
-
"*" (2 arguments): Multiplication. Result is the product of the two numbers.
-
"/" (2 arguments): Division. Result is the quotient of the two numbers.
-
"%" (2 arguments): Modulo. Result is the remainder when dividing the two numbers.
Behaves like JavaScript's % does, i.e. sign of the result is based on the sign of the first argument.
-
"mod" (2 arguments): Modulo. Result is the remainder when dividing the two numbers.
This uses "floored" modulo instead of "truncated" modulo, which means the sign of the result is based on the sign of the second argument.
For example, [-7, "%", 4] evaluates to -3 (taking the negative of 7 % 4),
while [-7, "mod", 4] evaluates to 1 (since -7 is one more than a multiple of 4, that being -8).
In my opinion, floored modulo is the "correct" modulo.
-
"^"/"**" (2 arguments): Exponentiation. Result is what you get when you raise the first argument
to the power of the second argument. (These two operators are synonyms, they do the same thing)
-
"log" (2 arguments): Logarithm. Result is the base-(second argument) logarithm of the first argument.
-
"round" (2 arguments): Rounding. Rounds the first argument to the nearest multiple of the second argument.
For example, [47.4, "round", 1] evaluates to 47, whereas
[47.4, "round", 10] evaluates to 50. (Yes, the second argument is required. There is no one-argument round operator.)
-
"floor" (2 arguments): Floor. Like round, but it always rounds down.
-
"ceil"/"ceiling" (2 arguments): Ceiling. Like round, but it always rounds up.
(These two operators are synonyms, they do the same thing)
-
"trunc" (2 arguments): Truncation. Like round, but it always rounds towards 0.
In other words, it acts like floor on positive numbers, it acts like ceil on negative numbers.
-
"abs" (1 argument): Absolute value. Result is the absolute value of the argument.
-
"sign" (1 argument): Sign. Result is 1 for positive numbers, -1 for negative numbers, 0 for zero.
(Infinity and -Infinity result in 1 and -1 respectively. NaN results in NaN.)
-
"sin", "cos", "tan":
Trig functions. All of these take 1 argument.
-
"gcd" (2 arguments): Result is the greatest common denominator of the two numbers.
Due to floating point shenanigans, you probably shouldn't use this on non-integers.
-
"lcm" (2 arguments): Result is the least common multiple of the two numbers.
Due to floating point shenanigans, you probably shouldn't use this on non-integers.
-
"factorial" (1 argument): Result is the factorial of the argument.
Does not work on numbers that aren't nonnegative integers.
-
"prime" (1 argument): Result is the nth prime, where n is the argument:
the 1st prime is 2, the 2nd prime is 3, the 3rd prime is 5, the 4th prime is 7, and so on.
[0, "prime"] results in 1. If the argument is negative, returns the negative of
what the positive version of that argument would give: [-4, "prime"] results in -7, for example.
Does not work on non-integers.
-
"expomod" (2 arguments): How many times can you divide the first argument by the second while keeping
it an integer? For example, [24, "expomod", 2] results in 3, since if you divide 24 by 2 three times it's
still an integer (3), but if you do so a fourth time it's not an integer anymore. Results in -1 if either argument is not an integer.
-
"bit&", "bit|",
"bit~",
"bit<<", "bit>>",
"bit>>>": Bitwise operators.
All of these take 2 arguments, except "bit~" which takes 1 argument.
-
"rand_int" (2 arguments): Returns a random integer between the two arguments (inclusive).
-
"rand_float" (2 arguments): Returns a random floating point number between the two arguments.
-
"defaultAbbrev" (2 arguments): Rewrites the number in the way that numbers are
typically displayed on tiles, in the score, etc.
Unlike the rest of the operators in this subsection, this operator results in a string instead of a number.
Numbers that are 10,000 or larger have commas put into them (four-digit numbers do not).
Numbers are rounded to three decimal places at most.
If a number is 1012 or larger, or it's smaller than 0.1 (and is not 0), then it is instead written
in scientific notation, with four decimal places of precision.
The scientific notation assumes that the number is being outputted to HTML, so the string you'd get would look something
like "1.43564 × 10<sup>24</sup>", since in HTML that displays as "1.43564 × 1024".
Comparison Operators
These operators don't have a set type: they will take arguments of any type, so they won't do type conversion before evaluation.
-
"=" (2 arguments): Equality. Results in true if the two arguments are equal,
results in false if they are not. Strict equality checking, like JavaScript's ===,
is used, so two values of different types are never considered equal even if, say, they're a number and a bigint
of the same number.
This does work on arrays: for example, if the two arguments are both the array [4, 5, 7],
then the result will be true. Two arrays are equal if and only if they have the same length and,
at every index, the elements at that index are equal.
-
"!=" (2 arguments): Not equals. Results in the opposite
of what "=" would return on these two arguments.
-
"<" (2 arguments): Less than. Results in true if the
first argument's value is less than the second argument's value, results in false otherwise.
Unlike "=", inequalities do work across types, so
[5n, "<", 6] will return true. (However, also unlike
"=", inequalities always return false on arrays)
-
">" (2 arguments): Greater than. Results in true if the
first argument's value is greater than the second argument's value, results in false otherwise.
-
"<=" (2 arguments): Less than or equal to. Results in true if the
first argument's value is less than or equal to the second argument's value, results in false otherwise.
-
">=" (2 arguments): Greater than or equal to. Results in true if the
first argument's value is greater than or equal to the second argument's value, results in false otherwise.
-
"min" (2 arguments): Minimum. Returns whichever of the two arguments is
less than the other one. If they are equal or inequalities don't make sense for these two values, returns the first argument by default.
-
"max" (2 arguments): Maximum. Returns whichever of the two arguments is
greater than the other one. If they are equal or inequalities don't make sense for these two values, returns the first argument by default.
Boolean Operators
These operators take boolean arguments and result in a boolean.
-
"&&" (2 arguments): AND. Results in true if both arguments are true
(or some value that type-converts to true), returns false otherwise.
-
"||" (2 arguments): OR. Results in true if at least one of the arguments is true
(or some value that type-converts to true), returns false otherwise.
-
"!" (1 argument): NOT. Results in the boolean negation of the argument.
-
"&&nsc", "||nsc" (2 arguments):
"&&" and "||" perform "short-circuit evaluation",
which means that if the result of the operator is already known after the first argument
(i.e. if the first argument is false for "&&" or if it's true for "||"),
the second argument is not evaluated at all. This is useful if, say, the first argument is making sure some number isn't zero and
then the second argument needs to divide by it. If the second argument is a CalcArray with side effects you want to happen,
such as changing a variable, then use these "nsc" ("no short-circuit") versions, which will evaluate the second argument
even if doing so cannot change the result.
String Operators
The first argument to these operators is a string, but the later argument(s) might not be;
unlike with number operators, where every argument was a number, string operators often do things that require some non-string arguments.
These operators are generally denoted by having "str_" at the front, to distinguish them from their array counterparts if they have one.
-
"str_char" (2 arguments): Results in a character of a string.
First argument is the string, second argument is the index (which is a number).
Remember that indices are 0-indexed, so ["hello", "str_char", 1] will result in "e".
-
"str_length" (1 argument): Results in the length of the string,
i.e. the amount of characters in the string (which is a number).
-
"str_concat" (2 arguments): Concatenation. Results in a string which
is the concatenation of the two arguments, i.e. what you'd get from adding the strings together in JavaScript.
-
"str_concat_front" (2 arguments): Concatenation, except in
the concatenated string the second argument is put before the first argument instead of after.
-
"str_slice" (3 arguments): Results in a slice of the string.
The latter two arguments are both numbers: the second argument is the index where the slice starts (this index is included in the slice),
the third argument is the index where the slice ends (this index is not included in the slice).
As in JavaScript, the arguments are allowed to be negative, where -1 is the last character of the string,
-2 is the second-to-last character of the string, and so on.
-
"str_substr" (3 arguments): Similar to "str_slice",
except instead of the third argument being the end index, the third argument is how many characters,
starting from the start index, are included in the slice.
-
"str_indexOf" (2 arguments): Results in the first index (a number)
of the second argument as a substring in the first argument. (The index resulted in is the
index that the first character of the second argument is at in the first argument).
Results in -1 if the second argument is not found as a substring of the first argument.
-
"str_lastIndexOf" (2 arguments): Like
"str_indexOf", except if the second argument occurs as a substring of the
first argument multiple times, the index resulted in is of the last occurance instead of the first occurance.
-
"str_indexOfFrom", "str_lastIndexOfFrom" (3 arguments):
Similar to the previous two operators, except there's a third argument which is a number.
This number is the index where the search begins, which means
"str_indexOfFrom" won't consider any occurances before that index,
whereas "str_lastIndexOfFrom" won't consider any occurances after that index,
in the search.
-
"str_includes" (2 arguments): Basically a boolean-resulting
version of "str_indexOf": results in true if the second argument is contained as
a substring in the first argument, returns false if it is not.
-
"str_splice" (4 arguments): Results in a string that's like the first argument,
but with some characters replaced with other characters (or potentially just removed).
The second argument (a number) is what index to start the replacement at, the third argument (a number) is how many characters
starting from that index to remove, and the fourth argument (a string) is what substring to insert into the string
in their place. If you wish to remove characters without inserting any, set the fourth argument to the empty string.
If you wish to insert characters without removing any, set the third argument to 0.
-
"str_toUpperCase", "str_toLowerCase" (1 argument):
Results in a string that is the argument but with any letter characters changed to their uppercase or lowercase versions
(depending on which operator, obviously).
-
"str_split" (2 arguments):
Results in an array where each element is a piece of the first argument string. The second argument is a string used as the
splitter: whenever that substring is encountered, that string element of the array ends, the splitter substring is skipped, and
the next string element of the array begins from there.
If the second argument is the empty string, the string is split at every character, so every character becomes an array element.
Literal Arrays and Array Operators
Normally, when there's an array inside a CalcArray, that inside array is also interpreted as a CalcArray.
If you want to create an actual array as a value to manipulate within a CalcArray, then you have to put
"@Literal" at the beginning of that array.
For example, putting [1, 5, 9] into a CalcArray will cause it to attempt
to evaluate that as a CalcArray (and 5 isn't a valid operator, so it will just return 1),
but if you put ["@Literal", 1, 5, 9] into a CalcArray, that will become the array
[1, 5, 9] as an array value that can be used within the CalcArray.
Any array inside a literal array is also treated as a literal array; you do not need to put "@Literal"
at the starts of the sub-arrays, only at the start of the external literal array. If you want an array inside a literal
array to be evaluated as a CalcArray, put "@CalcArray" at the start of the array:
for example, if you put ["@Literal", 1, [2, "+", 4], ["@CalcArray", 2, "+", 4]] into a CalcArray,
then the value that evaluates to is the array [1, [2, "+", 4], 6].
CalcArrays treat arrays as values, not as objects. This means that, like strings, every CalcArray operation on an array creates
a new array rather than mutating the old one, even operators like "arr_push" whose JavaScript equivalents mutate the existing array.
This also means that checking arrays for equality doesn't check if they're "the same object", it checks if all their elements are equal.
Inequalities still always return false on arrays.
Here are the operators whose first argument is an array.
These operators are generally denoted by having "arr_" at the front, to distinguish them from their string counterparts if they have one.
-
"arr_elem" (2 arguments): Results in an element of an array.
First argument is the array, second argument is the index (which is a number).
Remember that indices are 0-indexed.
-
"arr_length" (1 argument): Results in the length of the array,
i.e. the amount of elements in the array (which is a number).
-
"arr_indexOf" (2 arguments): Results in the first index (a number)
of the second argument as an array in the first argument.
Results in -1 if the second argument is not found as an element of the first argument.
-
"arr_lastIndexOf" (2 arguments): Like
"arr_indexOf", except if the second argument occurs as an element of the
first argument multiple times, the index resulted in is of the last occurance instead of the first occurance.
-
"arr_indexOfFrom", "arr_lastIndexOfFrom" (3 arguments):
Similar to the previous two operators, except there's a third argument which is a number.
This number is the index where the search begins, which means
"arr_indexOfFrom" won't consider any occurances before that index,
whereas "arr_lastIndexOfFrom" won't consider any occurances after that index,
in their search.
-
"arr_includes" (2 arguments): Basically a boolean-resulting
version of "arr_indexOf": results in true if the second argument is contained as
an element in the first argument, returns false if it is not.
-
"arr_copy" (1 argument): Creates a copy of the argument.
I'm not sure why you'd ever need this, seeing as any other array operator will also make a copy,
but I included it just in case. If you find yourself needing this operator, you've probably run into a bug,
so please let MathCookie17 know of the bug you found.
-
"arr_edit_elem" (3 arguments): The second argument is a number,
the third argument is an element of the array (so it can be of any type). Results in an array that's
the same as the first argument, except the element at the index indicated by the second argument is replaced with
the third argument. For example, [["@Literal", 10, 20, 30], "arr_edit_elem", 1, 25]
replaces the element at index 1 of [10, 20, 30] with 25, so it results in [10, 25, 30].
-
"arr_push" (2 arguments): The second argument is an element.
Results in an array that's the same as the first argument, but with the second argument added on as a
new element at the end of the array.
-
"arr_pop" (1 argument):
Results in an array that's the same as the first argument, but with its last element removed.
-
"arr_unshift" (2 arguments): The second argument is an element.
Results in an array that's the same as the first argument, but with the second argument added on as a
new element at the beginning of the array.
-
"arr_shift" (1 argument):
Results in an array that's the same as the first argument, but with its first element removed.
-
"arr_concat" (2 arguments): Both arguments are arrays.
Results in an array containing all the elements of the first argument then all of the elements of the second argument.
-
"arr_concat_front" (2 arguments): Both arguments are arrays.
Results in an array containing all the elements of the second argument then all of the elements of the first argument.
-
"arr_flat" (2 arguments): The second argument is a number.
This operator "flattens" an array, meaning that any sub-arrays inside it are broken up,
making their elements into elements of the outer array. Sub-arrays of sub-arrays are not affected by this
if the second argument is 1; the second argument is how many layers deep the flattening extends.
-
"arr_slice" (3 arguments): Results in a slice of the array.
The latter two arguments are both numbers: the second argument is the index where the slice starts (this index is included in the slice),
the third argument is the index where the slice ends (this index is not included in the slice).
As in JavaScript, the arguments are allowed to be negative, where -1 is the last element of the array
-2 is the second-to-last element of the array, and so on.
-
"arr_splice" (4 arguments): Results in an array that's like the first argument,
but with some elements replaced with other elements (or potentially just removed).
The second argument (a number) is what index to start the replacement at, the third argument (a number) is how many elements
starting from that index to remove, and the fourth argument (an array) is what elements to insert into the array
in their place. If you wish to remove elements without inserting any, set the fourth argument to the empty array.
If you wish to insert elements without removing any, set the third argument to 0.
-
"arr_reverse" (1 argument): Results in an array that's the argument
but with its elements in the opposite order.
-
"arr_binarySearch" (2 arguments): A version of "arr_indexOf"
that only works on an array sorted from least to greatest (meaning the elements have to be of a type that inequalities work on),
but uses an algorithm that runs faster.
-
"arr_binaryInsert" (2 arguments): First argument is an array that must be sorted from least
to greatest (meaning the elements have to be of a type that inequalities work on), second argument is an element.
Inserts that element into its proper place in the sorted array.
(Note: I do intend to add versions of binary search and binary insert that allow a custom comparison function someday)
-
"arr_eqRearrange" (2 arguments): For "=="
to result in true on two arrays, their elements must be the same in every position.
"arr_eqRearrange" just requires that they have
all of the same elements, even if they're not in the same order: in other words, if it's possible to
rearrange the elements of one of the arguments to get the other argument,
"arr_eqRearrange" will result in true.
It will result in false if they can't be rearranged into each other this way.
-
"weightedRandomArrayEntry" (2 arguments):
If you want to select a random element from a given array with equal odds, you'd typically do
[(the array in question), "arr_elem", ["@Parent -2", "arr_length", "-", 1, "rand_int", 0]]
(I'll explain what "@Parent -2" means later), but what if you want the entries to have different odds of being chosen?
That's what "weightedRandomArrayEntry" does: its first argument is the array to select a random element from,
its second argument is an array of numbers that are the weights of the elements of the first array in the random selection.
If the arrays are different lengths, then for the purposes of the random selection, both arrays will be treated as if they only contain
their first few elements up to the length of the smaller of the two arrays.
There's a few more advanced array operators that I can't explain yet, because they rely on variables, which I haven't discussed yet, to do their
work: "arr_sort", "arr_map", "arr_filter",
"arr_reduce", and "arr_reduceRight". These will be discussed later.
BigInt Operators
Putting a BigInt into a CalcArray works differently depending on where you're doing it. If you're
using CalcArrays in the Compendium directly (such as messing with the console or actually editing the code to make a mode),
then they work just as you'd expect: the BigInt of value 5 is 5n. However,
BigInts don't work nicely with JSON's stringify and parse
methods, which are used for save codes, so if you're editing a save code, they're entered differently:
the BigInt of value 5 is "@BigInt 5". These methods of entering BigInts are mutually exclusive:
5n won't work in a save code, and "@BigInt 5" won't work in the Compendium directly.
BigInt operators are generally the same as number operators, except they have a B on the end to indicate that they're the BigInt versions.
The following operators work the same as their number counterparts, the only change is that their arguments and result are BigInts:
"+B", "-B", "*B",
"%B", "modB", "^B"/"**B",
"absB", "signB", "gcdB", "lcmB",
"factorialB", "primeB", "expomodB",
"roundB" (remember, round has a second argument and it rounds the first argument to the nearest multiple of the second,
so rounding isn't useless here), "floorB", "ceilB"/"ceilingB"
(truncB currently doesn't exist, though I don't remember why I didn't add it), "bit&B", "bit|B",
"bit~B", "bit<<B", "bit>>B",
and "bit>>>B", and "rand_bigint" works the same as "rand_int".
"/B" and "logB" also exist.
Since the number versions of these operators can return decimals, their results are truncated here (remember, "truncated" means "rounded towards 0"):
for example, [14n, "/B", 3n] results in 4n, since 14 / 3 is between 4 and 5. Truncated division is how
division normally works with BigInts, so it shouldn't be a surprise that that's how it's done for division and logarithms here.
Be careful here: CalcArrays do not have any error handling built in, so if you do something that cause BigInts to throw an error,
like dividing by 0 or taking the logarithm of a negative number, the game will crash!
(though "logB" will not throw an error when given 0n as its first argument; it will result in -1n instead).
"defaultAbbrevB" exists too. It's assumed that if you're using a BigInt, you care about the exact value of the number
rather than just its size, so "defaultAbbrevB" never switches to scientific notation - the BigInt's digits are written out in full
(with commas if it has at least five digits), regardless of how many digits there are.
The only number operators that don't have BigInt counterparts at all are the trig functions and "rand_float",
since those four operators make no sense without non-whole numbers.
Several of the modes that do more advanced things with their numbers (1762, SQUART, X^Y, DIVE, and so on; basically any mode where the
exact values of the numbers, rather than just multiples and products of powers of numbers, are relevant), use BigInts instead of numbers.
This means that BigInts have some additional operators that do not have number equivalents:
-
"rootB" (2 arguments): Takes the (second argument)th root of the first argument,
truncated (rounded towards 0). Numbers didn't need a root operator since you could just use a decimal exponent,
but decimals don't exist for BigInts, so a root operator was needed to go alongside the log operator.
-
"perfectPowerFormB" (2 arguments): Both arguments are BigInts. Results in a three-entry array of BigInts representing
(the absolute value of) the first argument as a perfect power with the largest possible exponent, provided that exponent is no larger than the second argument.
In the array, the first entry is the base, the second entry is the exponent, and the third entry is the sign.
For example, [81n, "perfectPowerFormB", 10n] results in [3n, 4n, 1n] since 81 is 3^4, but
[81n, "perfectPowerFormB", 3n] results in [9n, 2n, 1n] since the second argument is too small to allow an exponent of 4.
If the first argument is 1n, 0n, or -1n, the resulting array is [abs(first argument), 0n, sign]; the 0n exponent is used to indicate that it's a special case
(since any exponent would work).
-
"primeFactorizeB" (2 arguments): Results in the prime factorization of the first argument.
The second argument can be 0, 1, or 2, and it changes the way the prime factorization is formatted.
Format 0 means the result is an array containing the exponents of 2, 3, 5, 7, 11, etc. in the prime factorization,
stopping after the last prime factor of the first argument: for example, factorizing 56n with format 0 will result in
[3n, 0n, 0n, 1n].
Format 1 means that the result is an array containing pairs of primes and their corresponding exponent,
from smallest prime to largest prime, omitting primes where the exponent is 0:
for example, factorizing 56n with format 1 will result in [[2n, 3n], [7n, 1n]].
Format 2 means that the result is an array containing the primes that multiply to the first argument,
including a prime multiple times if needed, sorted from smallest prime to largest prime:
for example, factorizing 56n with format 2 will result in [2n, 2n, 2n, 7n].
-
"primeDefactorizeB" (2 arguments): The inverse of "primeFactorizeB".
First argument is an array in a form that "primeFactorizeB" can return, second argument is
what format that array is in (0, 1, or 2), and the operator results in the BigInt that would factorize into that array if run through
"primeFactorizeB".
-
"factorAmountB" (1 argument): Results in the amount of positive factors that the argument has.
-
"factorListB" (1 argument): Results in an array of all the positive factors that the argument has,
from smallest to largest.
-
"basebit&B" (3 arguments): Bitwise AND, but the base isn't necessarily 2. First two arguments are the arguments
to the AND, third argument is the base. Takes the minimum digit between the two arguments at each place value to get the result.
-
"basebit&|B" (3 arguments): Bitwise OR, but the base isn't necessarily 2. First two arguments are the arguments
to the OR, third argument is the base. Takes the maximum digit between the two arguments at each place value to get the result.
-
"basebit~|B" (2 arguments): Bitwise NOT, but the base isn't necessarily 2. First argument is the argument
to the NOT, second argument is the base. To get the result, takes the first argument and replaces each of its digits in that base with
(base minus that digit).
-
"basebit^|B" (3 arguments): Bitwise XOR, but the base isn't necessarily 2. First two arguments are the arguments
to the XOR, third argument is the base. Adds (modulo the base) the digits of the two arguments at each place value to get the result.
These operators (aside from "rootB") don't have number versions because it's assumed
that if you're in a situation that calls for such an operator, then you're in a situation where you care about the number's precise value,
so you'd want to use BigInts anyway. (The only reason numbers even get "prime" is that that operator was
added before BigInt support was added to CalcArrays. If that weren't the case, anything to do with primes would be BigInt exclusive,
since if you're using numbers rather than BigInts you probably don't care about primes in that situation.)
BigRationals
In v2.1, a new number type was added to the 2048 Power Compendium: BigRational, exact-precision rational numbers,
which are stored as a numerator and denominator that are both BigInts.
BigRational is a class, so to make a BigRational with value 2/3, you do new BigRational(2n, 3n).
You can also just give a single BigInt or number instead of two
(if the argument is one number, continued fractions will be used to approximate a non-whole number as a fraction),
or even a string such as "2/3", as an argument to the BigRational constructor.
BigRationals are objects, but they're treated as if they're values: all of their methods create new BigRationals (so they do not
mutate the existing ones). All BigRational operations automatically simplify their fractions, so
new BigRational(1n, 3n).plus(new BigRational(1n, 6n)) will return a BigRational with value 1/2,
i.e. with a numerator of 1 and a denominator of 2.
BigRationals also support the three non-finite floating point values: 1/0 is Infinity, -1/0 is -Infinity (Infinity and -Infinity's
numerators simplify to 1 and -1), and 0/0 is NaN.
As with BigInts, you have to make BigRationals differently if you're editing a save code, since stringify
doesn't preserve function methods: in a save code, "@BigRational 2 3" will make a BigRational with value 2/3.
Like how BigInt operators have B on the end, BigRational operators have BR on the end. The following operators are
equivalents to number/BigInt operators that work as expected: "+BR",
"-BR", "*BR", "/BR",
"modBR" ("%BR" doesn't exist - since BigRational is a class I created, I only bothered
to add the floored modulo since that's in my opinion the correct one, not the truncated modulo),
"absBR", "signBR", "roundBR",
"floorBR", "ceilBR"/"ceilingBR"
(again, truncation isn't included here), "gcdBR", "lcmBR",
"roundBR", "expomodBR" (unlike with numbers and BigInts,
here the exponent can be negative: 3/8 has -3 factors of 2 in it, for example), and "perfectPowerFormBR".
"defaultAbbrevBR" writes BigRationals as mixed numbers.
There are also some BigRational operators that either don't have number or BigInt equivalents, or work differently than those equivalents:
-
"numeratorBR" (1 argument): Results in the numerator (a BigInt) of the argument.
-
"denominatorBR" (1 argument): Results in the denominator (a BigInt) of the argument.
-
"negBR" (1 argument): Results in the negation of the argument, i.e. multiplies the argument by -1.
Yes, you could just use "*BR", new BigRational(-1n) for this, but neg() was provided as a method in
the BigRational class (since BigRational was made in the style of break_infinity and break_eternity's Decimal classes),
so I figured I'd include it as a CalcArray operator too.
-
"recipBR" (1 argument): Results in the reciprocal of the argument. (Results in positive infinity
if the argument is 0).
-
"^BR"/"**BR" (2 arguments):
Exponentiation. The second argument is a BigInt instead of a BigRational, since rational exponents result in non-rational numbers.
BigRational was made so far as it was needed for the Power Compendium's use. As such, it does not include methods like roots, logs, or trig functions
at this time. Those operations don't return rational numbers - numbers and BigInts can have versions of them because they have limited "granularity"
(i.e. there is a nonzero step size between each possible value), but BigRationals can get as precise as needed, so a root, log, or trig function
would never reach a sufficiently exact answer. Such an operator would require an extra argument specifying a level of precision to stop the algorithm
at. I'll probably extend the BigRational class to include these operators someday, but for now they are not included (and even if they are added someday,
it'll probably be in a different project that uses BigRational, not in the Power Compendium).
BigRationals are used in a few places in the Power Compendium's code - places where both non-integer values and exact precision are needed.
They're most visibly used in the Partial Absorb variant of the mode 180, but they're also used for the colors of tiles in mod 27,
calculating the ratio between tiles in 3385, and a few other places.
GaussianBigInts
This is the other number type class that the Compendium uses that's not a native JS type. GaussianBigInts were actually added before BigRationals,
in v1.5, but I chose to mention BigRationals first since they're easier to understand and are a better example of these classes.
A GaussianBigInt represents a Gaussian integer, a complex number of the form a+bi for integers a and b.
As with BigRationals, you'd make a GaussianBigInt with value 2+3i via new GaussianBigInt(2n, 3n),
unless you're in a save code, in which case you'd do "@GaussianBigInt 2 3" instead.
The complex numbers aren't ordered, so inequalities don't work on them: inequalities on GaussianBigInts will always return false,
max/min on GaussianBigInts will throw an error.
GaussianBigInt operators have GB on the end. The following operators are equivalents to operators from the other number classes
and work as expected: "+GB", "-GB", "*GB",
"modGB", "negGB", "gcdGB",
"lcmGB", "expomodGB", and "defaultAbbrevGB".
The kind of number that GaussianBigInts are representing is more "exotic" than the kind that BigRationals are representing,
so there are more operators here that work differently:
-
"reGB" (1 argument): Results in the real component (a BigInt) of the argument.
-
"imGB" (1 argument): Results in the imaginary component (a BigInt) of the argument.
-
"/GB" (2 arguments): Division. Result is rounded componentwise towards 0, as with BigInts.
-
"/mGB" (2 arguments): Division. Result is rounded in a way that minimizes the norm of the remainder.
-
"^GB"/"**GB" (2 arguments):
Exponentiation. The second argument is a BigInt instead of a GaussianBigInt, since non-real exponents result in non-whole numbers.
-
"ipowGB" (1 argument): The argument is a BigInt, but the result value is a GaussianBigInt.
Results in i to the power of the argument.
-
"rot90GB" (1 argument): Results in the argument multiplied by i, i.e. rotated 90 degrees in the complex plane.
-
"rot270GB" (1 argument): Results in the argument multiplied by -i, i.e. rotated 270 degrees in the complex plane.
-
"conjGB" (1 argument): Results in the complex conjugate of the argument.
-
"normGB" (1 argument): Results in the norm (the square of the absolute value) of the argument, as a BigInt.
-
"normGGB" (1 argument): Results in the norm (the square of the absolute value) of the argument, as a GaussianBigInt.
-
"toFirstQuadrantGB" (1 argument): Multiplies the argument by the necessary power of i to rotate it into the first
quadrant of the complex plane (or the positive real axis, if it's purely real or purely imaginary).
-
"firstQuadrantUnitGB" (1 argument): Results in the power of i that "toFirstQuadrantGB"
would multiply the argument by.
-
"gaussian_prime" (1 argument): Result is the nth Gaussian prime, where n is the argument.
The Gaussian primes in this list are all in the first quadrant, are sorted by norm, and in the case of a tie, the primes in question
will be a+bi and b+ai, so the one with the larger real component is listed first.
-
"gaussianSort" (2 arguments): Compares the two GaussianBigInts under a particular ordering.
Result value is a number, either -1, 0, or 1, as is consistent with comparison functions for sorting in JavaScript.
Results in -1 if the first argument comes earlier in the ordering, results in 1 if the second argument comes earlier in the ordering,
results in 0 if the arguments are the same. The ordering is as follows:
first, sort by norm, from smallest to largest. If the two have the same norm, sort by quadrant: quadrant 1 comes earliest, then quadrant 2, then quadrant 3, then quadrant 4.
For these purposes, as in "toFirstQuadrantGB", the positive real axis is in quadrant 1, the positive imaginary axis is in quadrant 2,
the negative real axis is in quadrant 3, and the negative imaginary axis is in quadrant 4.
If the two are still tied, sort by "taxicab" value instead of Euclidean value: if the two GaussianBigInts are a+bi and c+di, then compare a+b and c+d,
smaller one comes earlier.
If the two are still tied after that, then they must be a+bi and b+ai, or they must be equal. If they are a+bi and b+ai, the one with the higher real part
comes earlier.
Finally, if they're still tied after all of that, they're the same number, so result in 0.
GaussianBigInt isn't as versatile as BigRational, so as of now it's only used in one place in the 2048 Power Compendium:
in the waves mode Gaussian DIVE.
Other Operators
And now for the operators that don't fall under one of the above categories.
First, there's the type conversion operators, which all take 1 argument: "Number", "String",
"Boolean", "Array", "BigInt", "GaussianBigInt",
and "BigRational", which each convert the argument into their respective type.
"Number" on a GaussianBigInt will return 0 unless the GaussianBigInt is pure real, while
"Number" on a BigRational works properly (i.e. converting the BigRational 3/2 to a number gives the number 1.5).
Unlike in JavaScript, arrays converted to strings in CalcArrays will include the brackets on the edges of the array.
A GaussianBigInt converted into a string will be written as "a+bi" or "a-bi" where a and b are the component numbers.
A BigRational converted into a string will be written as a (potentially improper) fraction, unless the denominator is 1 (in which case it's written
as a whole number) or 0 (in which case it's written as "Infinity", "-Infinity", or "NaN").
"Boolean" on a GaussianBigInt or BigRational will always result in true, since they're technically objects.
"Array" results in a one-element array
where the element is the argument (unlike the implicit type conversion, the "Array" operator does this
even if that element was itself an array).
"BigInt" will, if the value can't be converted to a BigInt, try rounding it first, and if it still fails
(such as if you're converting a string, not a number, and that string can't become a BigInt itself), will default to 0.
Likewise, "GaussianBigInt" will default to 0+0i if the argument can't be converted correctly,
while "BigRational" will default to 0/0 (NaN) if the argument can't be converted correctly.
There's also "typeof", which takes 1 argument and results in the type of that argument as a string:
"number", "string", "boolean", "array", "bigint", "gaussianbigint", or "bigrational".
(CalcArrays don't have tools built in to handle the value undefined,
so it's recommended to avoid writing CalcArrays that could get undefined involved, but if it shows up anyway,
"typeof" will still return "undefined" on it.)
There's a couple simple ones that just return one of the arguments, ignoring the other one:
-
"1st"/"ignore" (2 arguments): Results in the first argument.
Useful if you want the second argument to do some side effect like changing a variable, but not affect the running value directly.
For the sake of readability, it's recommended to use "1st" when the second argument has a side effect,
while it's recommended to use "ignore" if you're using the second argument to leave a comment in the CalcArray.
(P.S. Simply returning the first argument is also the default action when something other than a valid operator is in
an operator position in a CalcArray)
-
"2nd" (2 arguments): Results in the second argument.
Useful if you want to use the CalcArray to do manipulations with variables and then replace the running value with one of these variables at the end.
"announce", "output", and "console.log"
all display their second argument somehow then result in their first argument.
"announce" displays the second argument as a message on the screen; this is how DIVE shows its
messages about seed unlocks and eliminations. "announce" takes three arguments; the third argument is
how many milliseconds the announcement lasts for.
The other two only take two arguments.
"output" converts the second argument to a string and places it as a text element at the bottom of the page,
while "console.log" logs the second argument to the console. "output" and "console.log"
should only be used for testing/bugfixing, not in a finished mode.
"defaultAbbrevAny" is a typeless version of the other defaultAbbrev operators, which will call one of the four of those
depending on the type of the argument (it will leave the argument unchanged if it's not one of the four numeric types).
"@primesUpdate" (2 arguments) updates the array of prime numbers that the Compendium currently has stored so that it contains every prime
up to at least the second argument, and then it results in the first argument (so it leaves the CalcArray's running value unchanged).
There's a couple operators that evaluate CalcArrays within a CalcArray.
"CalcArray" takes 1 argument, a literal array, and evaluates it as a CalcArray.
"CalcArrayParent" takes 2 arguments, where the first is of any type and the second is a literal array,
and "applies" the second argument as a CalcArray to the first argument, i.e. evaluates a CalcArray that's the second argument but with the first argument
unshifted onto the second argument as its first element. For example, [1, "CalcArrayParent", ["@Literal", "+", 2]]
applies the ["+", 2] as if it's a function with 1 as the input, so it evaluates [1, "+", 2],
resulting in 3.
DIVE turned out to be a complicated enough mode that it needed an operator added specifically for it:
"DIVESeedUnlock", which takes three arguments.
"DIVESeedUnlock"'s first argument is a bigint, its second argument is a list of bigints, and its third argument is a number (either 0, 1, 2, 3, or 4).
"DIVESeedUnlock" checks the first argument as a new tile being made in DIVE to see if it would unlock a new seed.
The second argument is the list of existing seeds to try dividing it by. The resulting value is what new seed would be unlocked (if it returns 1n, that means
no unlock, since the first argument can be fully divided by the existing seeds).
The third argument is the mode to do the checks in: mode 0 checks the seeds largest to smallest, mode 1 uses the recursive algorithm the original DIVE uses that ensures the minimum
possible outcome (but this theoretically runs in exponential, or perhaps factorial, time with respect to the number of seeds, so it could get quite laggy,
though you shouldn't run into lag with it in a normal DIVE game), mode 2 checks the seeds smallest to largest, mode 3 checks them in the order they already are
in the list, and mode 4 uses the recursive algorithm but to ensure the maximum possible outcome (while still obeying the "can't be divided by any of the seeds anymore" rule)
instead of the minimum.
Many of the waves modes use "DIVESeedUnlock", but Gaussian DIVE needed its own variant: "GaussianDIVESeedUnlock",
which is like "DIVESeedUnlock" but using GaussianBigInts
instead of BigInts; "GaussianDIVESeedUnlock" takes four arguments, with the fourth being a boolean that determines whether the
result should be rotated into the first quadrant (if true) or left as is (if false).
There's a third one of these, "CustomDIVESeedUnlock", which I will discuss later once we've learned about variables.
Part 3: Other CalcArray Features
Conditionals and Loops
The string "@if" is placed in a CalcArray in the position that an operator would be, but it's not
considered an operator itself. "@if" creates an if statement: the next entry of the CalcArray after the
"@if" should be a CalcArray that would result in a boolean, and then the terms after that (the first of which should be an operator itself,
and continue the CalcArray from there) will only be applied if that boolean CalcArray expression returned true.
The if statement lasts until an "@end-if" is reached.
For example, in [3, "@if", ["@This 0, "=", 4], "*", 4, "+", 2, "@end-if", "-", 1],
if ["@This 0, "=", 4] results in true (more on what "@This 0" means later),
then the *4 and the +2 will be applied, so the CalcArray will result in 13. If ["@This 0, "=", 4]
results in false, then the *4 and the +2 will be skipped since they're inside the if statement, but the -1 will still be applied,
so the CalcArray will result in 2.
To go along with "@if", there's also "@else" and "@else-if".
Each of these works similarly to "@if" in that the terms after them are considered part of their statement until an
"@end-else" or "@end-else-if" (respectively) is reached.
An "@else" or "@else-if" statement will be skipped unless the most
recent "@if" or "@else-if" statement in this CalcArray had its boolean
expression return false, and there hasn't been another "@else-if" or "@else"
checked since the most recent false-resulting "@if" or "@else-if" check.
An "@else" statement does not have a boolean-resulting CalcArray after the "@else":
if the most recent "@if" or "@else-if" boolean resulted in false, the
"@else" statement is definitely triggered, and the first term after the "@else"
should be the operator that starts the "@else" statement.
"@else-if", like "@if", does have a boolean CalcArray as the first element after the
"@else-if", so for an "@else-if" statement to be applied, the most recent
"@if" or "@else-if"'s boolean expression must have returned false, and the
"@else-if"'s boolean expression must return true.
To make loops, you use "@repeat". The term after a "@repeat"
should be either a number, or a CalcArray that results in a boolean (if it's a number it needs to be a plain number,
not a CalcArray that results in a number), and the terms after that is the CalcArray segment to apply repeatedly;
the end of a looping segment is denoted by "@end-repeat". If the term after the
"@repeat" is a number, then that number is the amount of times that the loop is run.
If the term after the "@repeat" is a CalcArray, then that CalcArray will be run
before each loop, and the loop will only continue if that CalcArray results in true.
Of course, these conditional and loop statements can be nested inside each other - so make sure you put your "@end-if"s,
"@end-repeat"s, etc. in the right places, or things will get buggy!
If you need to exit all your statements at once, there's "@end-stack", which marks the end of all ifs, elses, else-ifs, and repeats
it's inside at once (though in the repeat case it doesn't forcefully end it, the loop will keep going until it ends as usual).
"@end-stack" is currently unused in the Compendium, and I don't foresee it being used anytime soon, so it's currently
pretty much untested - so it might not work anyway.
Parents
Strings with an @ at the beginning of them tend to do special things in a CalcArray.
These can be special operator-like tools, like conditionals and loops, but they can also be stand-ins
for values that will be evaluated when it comes time to evaluate them. "@Parent" strings are one example of this.
An "@Parent" string is a way to reference the running value of the current CalcArray or of one of the parent CalcArrays it's inside.
"@Parent -1" will, at evaluation time, be replaced with whatever the running value of the current CalcArray is.
"@Parent -2" will be replaced with the running value of the CalcArray that the current CalcArray is inside (if one exists),
"@Parent -3" will be replaced with the running value of the CalcArray two layers up, and so on.
These work like the indexes in the .at() method for arrays, so while negatives go from the inside out, positives go from the outside in:
"@Parent 0" refers to the running value of the outermost CalcArray that this CalcArray is in some nested layer of,
"@Parent 1" to one layer within that, and so on. The nonnegative indices are currently unused in the Compendium -
the negative indices are much more useful, since their behavior is less dependent on how many layers deep in CalcArrays they're in.
As an example, take [3, "+", 8, "*", [2, "+", "@Parent -2"], "-", 7].
The 3+8 is evaluated first, turning it into [11, "*", [2, "+", "@Parent -2"], "-", 7].
Now the inner CalcArray is evaluated, and the "@Parent -2" refers to the running value of the CalcArray outside the inner one,
which in this case is 11, so it becomes [11, "*", [2, "+", 11], "-", 7],
which becomes [11, "*", 13, "-", 7], which becomes [143, "-", 7],
and thus the result is 136.
Replacing an @Parent string with the appropriate value does not happen until
the operator where the @Parent string is an argument is reached in the CalcArray's process.
The replacement is not permanent: if this is inside a loop, then the @Parent will be re-evaluated
each time it's reached.
Variables
Normally, the only changing value that a CalcArray stores is its "running value" (its current first argument), as well as being able to access the
running values of its parent CalcArrays via @Parent strings. But those aren't the only changeable values
that a CalcArray can work with: you can also add changeable variables into a CalcArray and work with those.
Variables in a CalcArray are stored in an array that the CalcArray works with internally.
By default, this array is empty. The typical way to add variables to a CalcArray is at the start, before the CalcArray begins properly.
To do this, begin the CalcArray by having its first few elements be the variables, then put in "@end_vars",
and then have the proper CalcArray part from there.
For example, the CalcArray [3, "aaa", true, 8, "@end_vars", 4, "+", 5]
will have [3, "aaa", true, 8] as its array of variables, then it will evaluate [4, "+", 5] and result in 9.
Of course, variables are useless if you don't access them. To access a variable, use an "@Var" string.
For example "@Var 0" becomes the variable at index 0 of the variables array,
"@Var 1" becomes the variable at index 1 of the variables array,
"@Var -1" becomes the last variable of the variables array,
"@Var -2" becomes the second-to-last variable of the variables array, and so on.
For example, in [1, 2, 3, 4, "@end_vars", 5, "*", "@Var 2"],
the variables array becomes [1, 2, 3, 4], and then it evaluates [5, "*", "@Var 2"];
the variable at index 2 is 3, so this becomes [5, "*", 3] and results in 15.
As with @Parent strings, @Var strings are only replaced with
a value when it's time to evaluate them, and are re-evaluated on each loop if applicable.
To change the value of a variable once it's been created, use "@edit_var" a special operator with
three arguments. The second argument is the index of the variable to edit, the third argument is the value to set that variable to.
The first argument becomes the result, so that "@edit_var" just edits the variable without impacting the
running value.
For example, [1, "@edit_var", 2, 3, ...] sets the variable at index 2 to the value 3, then the 1
continues as the running value.
There are other similar special operators associated with variables:
-
"@add_var" (2 arguments): Adds the second argument as a new variable at the end of the variables array,
results in the first argument.
-
"@insert_var" (3 arguments): Inserts the third argument as a new variable, with the second argument
being the index to insert it at (the variables after that index are shifted to make room for the new one, like splicing an array).
Results in the first argument.
-
"@remove_var" (2 arguments): Removes a variable from the variables array,
with the second argument being the index of the variable to be removed (the variables after that index are shifted to
close the gap, like splicing an array). Results in the first argument.
Normally, the variables array is local to that specific CalcArray, so children or parents of that CalcArray will not have access
to that CalcArray's variables. This is often undesired, because often when using "@edit_var"
you want to have the variable's new value be based on its current value, which means you need to access the variable's current
value inside a child CalcArray. To allow for this, put "@var_retain" at the beginning of a CalcArray
(before the list of variables if it has one), which causes that CalcArray to inherit the variables array from its parent
(it'll be the same object, so changes to the variables array made in the child will also affect the parent's variables array).
For example, [..., "@edit_var", 1, ["@var_retain", "@Var 1", "*", 2], ...]
will change the value of the variable at index 1 to double its current value; if the "@var_retain" wasn't there, the
child CalcArray wouldn't retain the variables of its parent, so "@Var 1" wouldn't find anything since that child CalcArray
would have no variables.
You could instead use "@var_copy", which does something similar but makes a copy of the variables array
instead of transferring it outright (so changes the child makes to the variables array won't transfer back to the parent), but I
find that usually "@var_retain" is what you want.
If your CalcArray has a lot of nested layers, putting in a bunch of "@var_retain"s can get annoying quickly,
so there's a shortcut: if you put "@global_var_retain" at the beginning of a CalcArray, then not only will
it retain the variables from its parent, the variable retaining will automatically cascade to all of its children, and all of its childrens' children,
and so on. Likewise, there's "@global_var_copy", and there's also "@global_var_none",
which stops a global_var cascade coming from its ancestors from applying to that CalcArray or its children.
Finally, there's also the "game variables"; whereas most variable arrays are local to a specific CalcArray, the game variables are a single array
that exists across the whole mode (and is typically initialized before the game starts by the code to set up the mode being played)
and can be accessed by any CalcArray. Use "@GVar 0", "@GVar 1",
"@GVar -1", "@GVar -2" and the like to access their values, and use
"@edit_gvar", "@add_gvar", "@insert_gvar",
and "@remove_gvar" to alter them. Since game variables are global, there's no need for a
"@var_retain" equivalent, but there sort of is one anyway:
if you put "@include_gvars" at the beginning of a CalcArray, then the current values of the game variables
will be copied into the beginning of the variables list in that CalcArray.
"@include_gvars" was added before "@GVar" strings, so it's an outdated feature you probably shouldn't use
(just use "@GVar" strings to acces them), but I still had to mention it.
Array Operators with CalcArray Arguments
Remember those five array operators I mentioned earlier as being too complicated to discuss yet?
That was because using them requires an understanding of variables, so now I can tell you how they work.
Each of these operators has one of its arguments be a CalcArray expression; what that expression does depends on the operator,
but in all of these cases, it will be run multiple times.
These expressions themselves will have "inputs" that come from the array being operated on (these inputs change on the different runs
of the expression), and the way this is accomplished is by adding those inputs as variables at the end of the variables array
of that CalcArray expression, so within the expression you use "@Var -1", "@Var -2",
etc. to access their values.
Here are the five operators in question:
-
"arr_sort" (2 arguments): The first argument is an array, the second argument is a CalcArray expression.
Sorts the array, using the CalcArray expression as a comparison function. The comparison function compares two elements, which
inside the expression are "@Var -1" and "@Var -2".
The comparison CalcArray should result in a negative number if "@Var -2" should come before "@Var -1"
in the sorted array, it should result in a positive number if "@Var -2" should come after "@Var -1"
in the sorted array, and it should result in 0 if the two are considered equal (i.e. it doesn't matter what order they go in).
The comparison function must return a number, not a bigint or another numeric type.
For example, [["@Literal", 1, 5, 4, 2, 3], "arr_sort", ["@Var -2", "-", "@Var -1"]] sorts the array by numeric value from
least to greatest, resulting in [1, 2, 3, 4, 5].
-
"arr_map" (2 arguments): The first argument is an array, the second argument is a CalcArray expression.
Replaces each element of the array with the value that that CalcArray expression results in.
Inside the CalcArray expression, "@Var -1" is the element currently being operated on,
and "@Var -2" is the index of that element in the array.
For example, [["@Literal", 1, 5, 4, 2, 3], "arr_map", ["@Var -1", "+", 5]] adds 5 to each element of the array,
resulting in [6, 10, 9, 7, 8].
-
"arr_filter" (2 arguments): The first argument is an array, the second argument is a CalcArray expression.
The second argument should return a boolean; the result of this operator is an array containing only the elements of the first array where
the CalcArray expression resulted in true.
Inside the CalcArray expression, "@Var -1" is the element currently being operated on,
and "@Var -2" is the index of that element in the array.
For example, [["@Literal", 1, 5, 4, 2, 3], "arr_filter", ["@Var -1", "%", 2, "=", 1]] only keeps the odd
numbers in the array, removing the even ones and resulting in [1, 5, 3].
-
"arr_reduce" (3 arguments): The first argument is an array, the second argument is some value, and the third argument is a CalcArray expression.
Combines all the elements of the first argument into some result value, using the third argument as the function to do so.
The second argument is the starting value, and each time the third argument is evaluated, the second argument is automatically put at the start of the CalcArray
before the evaluation begins.
Inside the CalcArray expression, "@Var -1" is the element currently being operated on,
and "@Var -2" is the index of that element in the array.
For example, [["@Literal", 1, 5, 4, 2, 3], "arr_reduce", 0, ["+", "@Var -1"]] starts at 0 and adds each element to the running total,
resulting in 15. Notice how the CalcArray expression begins with an operator, because the current running total is inserted at the start of the CalcArray
in each evaluation.
-
"arr_reduceRight" (3 arguments): Same as "arr_reduce", except
whereas "arr_reduce"'s run starts at the 0th element of the array and goes forwards through the array,
"arr_reduceRight"'s run starts at the last element of the array and goes backwards through the array.
And now for perhaps the most complicated operator of all:
"CustomDIVESeedUnlock", a very complicated version of the DIVESeedUnlock operators that lets you customize how it works,
allowing you to use the DIVE seed unlocking algorithm on things that aren't just BigInts or GaussianBigInts, with your own definitions as what counts for things like division.
This operator takes a whopping eleven arguments. The first three arguments do the same thing as they do in the other two DIVE seed unlock operators, while the rest of
them all represent functions, and thus have you use "@Var -1" and sometimes "@Var -2" to represent the
argument(s) to those functions. Here's what the rest of the arguments do:
-
The fourth argument is a two-argument function that defines what multiplication means in this context.
-
The fifth argument is a two-argument function that defines what division means in this context.
-
The sixth argument is a two-argument function that defines whether its first argument is considered "divisible" by its second argument.
-
The seventh argument is a two-argument function that's used to compare its arguments for sorting purposes, like how the comparison function
in "arr_sort" works.
-
The eighth argument is a two-argument functions that defines whether two values are considered coprime in this context.
(You can set this to just return false if you don't have a good meaning for it, though this may make modes 1 and 4 run slower!)
-
The ninth argument is the value used for the multiplicative identity 1.
-
The tenth argument is a one-argument function that defines whether a value is considered valid (like how in DIVE it won't run non-BigInt tiles like Garbage 0s through the algorithm).
-
The eleventh argument is a one-argument function that defines whether a value is considered equal to 1 (so it can be eliminated from the seeds list
for the checking purposes, since otherwise an infinite loop would ensue).
"CustomDIVESeedUnlock" is used in a couple waves modes with wacky seed unlock behaviors,
such as Dual-Tile DIVE (which needs "CustomDIVESeedUnlock" so it can do its multiplications, divisions, etc.
in Z2).
Part 4: How CalcArrays are Used in Modes
CalcArray()'s Other Arguments
So far, everything we've discussed has been within the CalcArray, i.e. the primary argument (argument #0, since the JS arguments array is 0-indexed)
to the JS CalcArray() function.
But that's not the only argument CalcArray() can take (though it is the only required one)!
Arguments #1 and #2 to CalcArray() make it so it's called "on a specific tile":
argument #1 is the vertical coordinate of that tile, argument #2 is the horizontal coordinate of that tile.
In the Power Compendium's grid, increasing the vertical coordinate moves downwards, increasing the horizontal coordinate moves rightwards.
These are both considered 0 by default.
Arguments #3 and #4 establish the direction of movement. Argument #3 is the vertical component of the movement direction,
argument #4 is the horizontal component of the movement direction.
These are both considered 0 by default.
Argument #5 is an array of additional arguments (it was made to be an array so that if I add any more info later on, I won't have to mess with
the order of the arguments). As of now, this array has meanings for up to three arguments: index 0 has the length of the current merge if one is occuring,
index 1 has the maximum spaces per move of the current movement direction, and index 2 has the "move type" (I think this is used for something related to
automatic moves, though I don't remember what exactly it distinguishes).
This argument is [1, Infinity, 0] by default.
Argument #6 is the grid of tiles that is being worked on. The default here is the normal grid; when something else is being used for this argument,
it's usually something like the array of next spawning tiles.
Arguments beyond that probably shouldn't be messed with even if you're writing code for the Compendium,
unless you're writing a function that's related to the running of CalcArrays themselves or something along those lines,
as they're data CalcArrays pass between themselves for recursion purposes and the like. But, for completeness's sake,
here's what they do anyway: argument #7 is the array of parent values, argument #8 is the variables array,
argument #9 is the "global variable stat" ("@global_var_retain" sets this to 1,
"@global_var_copy" sets this to -1, "@global_var_none" sets this to 0),
and argument #10 is an argument called "inner" that's usually true; this argument determines whether this actually counts as a child CalcArray
(thus adding its running value to the parents chain) or not (if, else, else-if, and repeat do a recursion call but without actually counting as a child CalcArray).
If you're making a 2048 Power Compendium mode, you'll be writing most of your "code" in CalcArrays themselves, so you shouldn't be worrying about
calling the CalcArray() function yourself - that's usually left to the "engine", although sometimes certain modifiers
(like random goals) do have to deal with this. However, understanding what data a CalcArray tracks will be useful for the rest of this part.
Internal Representations of Tiles
Before I can explain how things like tile display rules and merge rules work, I have to explain what a tile actually is internally.
I believe most 2048 variants create a Tile class for this kind of thing, but my mentality is usually "don't make a new class unless you have to".
Tiles don't really have a need for methods and such - all that's important to a given tile is its value(s) and its position.
As such, in the 2048 Power Compendium, tiles are just arrays, usually of numbers.
For example, in 2187, a tile is a two-element array, where the first number is the power of 3 it is and the second number is what that power of 3 is multiplied by.
For example of example, 162 is 34 times 2, so in 2187 the 162 tile internally is [4, 2]. Most Page 1 modes follow this pattern (with the base of the power part changed, of course).
Different modes represent tiles in different ways internally. Here are some examples:
-
In 2048 there's only one tile per power of two, so the array only has the 2x entry.
For example, the 1024 tile is [10] internally.
-
In 2584, the tiles also only have one entry. That entry is their index in the Fibonacci sequence,
with 1 being at index 0, so 1 is [0], 2 is [1], 3 is [2], 5 is [3], 8 is [4], and so on.
-
In 1535 1536 1537, the first entry is the n in 3 × 2n, the second entry is what to add to that,
which will be either -1, 0, or 1. For example, 95 is [5, -1], and 193 is [6, 1].
-
In 2700, tiles have three entries, representing 2first entry × 3second entry × 5third entry.
For example, [1, 2, 3] is the 2250 tile.
-
In 2058, tiles have three entries. An [a, b, c] tile represents ab × (a + 1)c:
for example, [3, 5, 2] is 35 × 42 = 3888.
-
Modes where every integer is possible, such as 1762 and 1321, or modes where the exact values of tiles
matter in a way that can't be simply reduced to power rules, like SQUART and 3385, often represent tiles as a
single-entry array containing a BigInt, so a 40 tile would be [40n].
In (232, 240) there are two BigInts since tiles are two numbers, so a (3, 4) tile is [3n, 4n].
-
In Bicolor 2187, the first entry is still the power of 3, but now red tiles get 1 for their second entry,
blue tiles get -1 for their second entry, and tiles that are double a power of 3 still get 2 for their second entry.
For example, a red 9 is [2, 1], a blue 9 is [2, -1], and an 18 is [2, 2].
-
In Isotopic 256, the first entry is the power of 2 like it is in 2048, but there's also a second
entry that stores that tile's remaining time left: for example, a 32P tile with 15 turns left would be [5, 15].
Stable tiles have that second entry set to 10300, since that's effectively infinite and
Isotopic 256 was added to the Compendium before save codes were updated to be able to handle the actual floating point number Infinity.
-
In Ratio-Fill 1296, tiles have three entries, except the second one is itself an array.
The first entry is the power of 6 it is, the second one is an array of five booleans that store which ratios
have already been filled, and the third one is the tile's number as a BigInt (because in this case calculating it from the other parts every time
a merge is attempted would have been too much hassle, so it's stored directly in the tile's array instead).
Of course, I didn't give every notable example here - there are some other interesting ways tiles are represented, so if you're interested
in examining the Compendium's code, you might want to go through some modes and see how they store their tiles.
These first two sections of Part 4 haven't really been about CalcArrays, have they?
I included them here because they provide context that's needed for what comes next.
Other Special Strings
@Parent, @Var, and @GVar strings
aren't the only special strings that CalcArrays can refer to. Most of the rest of them refer to in-game objects,
which is why I've been putting them off until now. Here's a list of them:
-
@This strings are probably the most important one: they refer to the element at that index
of the current tile. For example, if the tile at the coordinates the CalcArray's second and third arguments are pointing to is
[3, 6, 2], then "@This 0" evaluates to 3, "@This 1" evaluates to 6, and
"@This 2" evaluates to 2. Unlike @Parent and @Var
strings, negative indices won't work for @This strings. If you wish to get the entire array of the current tile
at once, use "@This", without any number.
-
@Next strings take two indices instead of one, and they refer to tiles subsequent to the
@This tile in the current direction. The first index is the amount of moves in that direction,
the second index is the index in that tile's array. For example, if the current movement direction is 2 to the left,
then "@Next 1 0" evaluates to index 0 of the tile 2 left from the current tile,
"@Next 2 3" evaluates to index 3 of the tile 4 left from the current tile,
and "@Next -1 1" evaluates to index 1 of the tile 2 right from the current tile.
If you want the entire array of one next tile, include the first number but not the second, such as "@Next 1".
If you want an array of all the next tiles up to the length of the current merge, use "@Next".
"@Next FL" is like "@Next", but it ignores the merge length and
continues all the way to the edge of the grid. "@Next" and "@Next FL"
will only include tiles in a positive multiple of the movement direction from the current tile, i.e. those whose first @Next index is positive.
-
@NextNE strings act the same as @Next strings, except when counting next tiles
from the current tile, they skip over empty tiles. @NextFull strings are like @NextNE strings,
except they also skip over holes in the grid. (Note that all @Next variants, including the original, will skip over
slippery tiles). "@NextNE FL" and "@NextFull FL" are not implemented as of now.
-
I'll note here that in @This, @Next, @NextNE, and @NextFull
strings, you can replace the "index within the tile" index (first index for @This, second index for the other two)
with @VCoord, @HCoord, or @Position to have it evaluate to the vertical coordinate, the horizontal coordinate, or a two-element array containing
both coordinates respectively, of that current or next tile. For example, "@Next 2 @VCoord" evaluates to
the vertical coordinate of the tile two tiles in the movement direction from the current tile. This is needed because, thanks to slippery tiles,
we can't necessarily just add the movement direction twice to the current tile's coordinates to get that next tile's coordinates.
-
@Relative strings have three indices: the first two are the grid coordinates relative to the current tile,
the third is the array index within the tile. For example, "@Relative -3 1 2" evaluates to the entry at index 2 of the tile
3 up and 1 right from the current tile. @Grid strings are similar, but they ignore the current tile and just looks at
those coordinates of the grid, so "@Grid 4 1 3" evaluates to the entry at index 3 of the tile 4 down and 1 right
from the top-left tile of the grid (since the top-left is (0, 0)).
With @Relative strings you have to give either two or three indices (two results in a whole tile, three in one entry of that tile),
but with @Grid strings you can give as few or as many as you want (one results in a whole row, zero gives the whole grid,
four would work if an element of a tile is itself an array, etc.)
-
The following special strings give you the CalcArray's other arguments: "@VCoord" and "@HCoord"
evaluate to the vertical and horizontal arguments the CalcArray is running at (arguments #1 and #2), "@VDir" and
"@HDir" evaluate to the vertical and horizontal components of the current movement direction (arguments #3 and #4),
"@MLength", "@SlideAmount", "@MoveType"
evaluate to their corresponding entries in argument #5 (the length of the current merge, the maximum spaces moved per move, and the move type),
and "@TileContainer" evaluates to whatever "grid" the CalcArray is being called on (argument #6; note that
while @This, @Next, etc. all work within the appropriate tile container,
@Grid strings always look at the actual grid regardless of if the CalcArray's argument #6 is some other container!)
-
@MVar strings are like @GVar strings, but they refer to the modifier variables,
which are set by the global modifiers rather than by the mode. Currently the only modifier setting that uses this is "To merge tiles, you must move in the same direction twice in a row.".
-
The following strings take no indices and evaluate to some statistic tracked during the game:
"@Score" (the score), "@Moves" (how many moves have been made up to this point),
"@Merges" (how many merges have occurred up to this point), "@MergeMoves"
(how many moves where at least one merge occurred have been made up to this point), and "@MergesBefore"
(Like "@Merges", except it only updates at the end of a move instead of whenever merges occur).
-
The following strings evaluate to some array of tiles tracked during the game, and you can add indices to them to return a single tile (with one index) or a
single element of a single tile (with two indices) and so on:
"@DiscTiles" (an array of all tiles discovered this game), "@DiscWinning" (an array of the tiles
that satisfy the mode's win condition), "@DiscLosing" (an array of the tiles that satisfy the mode's premature loss condition),
"@NextSpawns" (an array of the tiles that are next in the spawn order; the length of this array is equal to the Visible Next Spawned Tiles modifier,
unless that modifier is 0, in which case the length of this array is 1 but its only entry is an empty tile)
-
"@Primes" evaluates to the array of currently calculated prime numbers, as BigInts. Use the operator "@primesUpdate"
to update this. "@Primes" does not accept any indices, since you can just use the operators
prime or primeB if you want a single entry instead of the whole list.
-
"@TileOrder" evaluates to the order of the coordinates in which the tiles are being moved on this current move.
You shouldn't need this unless you're doing something exotic enough that you have to implement a form of merging yourself instead of using the normal methods,
like the secret mode with spoiler code [SPMAG] does. The result of this operator is an array of pairs, where each pair is a pair of coordinates,
with earlier entries meaning those coordinates come earlier in the merge order.
-
The following strings don't evaluate to anything special themselves (i.e. they remain as that string in a CalcArray), but they're the strings used by special
kinds of tiles and thus still have some special behaviors: "@Empty" for empty spaces, "@Void"
for holes in the grid, "@Slippery" for slippery tiles, and "@TemporaryHole n", where n is a number,
for a temporary hole that will last for n more moves. Note that these kinds of tiles are not arrays like the rest of the tiles are, they're just the strings.
Moving block tiles and Garbage 0s are not explicitly "special" tiles internally; those modifiers add new tiles to the regular tile types and modify
the merge rules to include them.
Color Expressions
A color expression is an array similar to a CalcArray that represents some color. Instead of the CalcArray()
function, these are evaluated via evaluateColor(); the first argument of that function is the color expression, the next two are the vertical and horizontal
coordinate, but then the next one is the grid/tile container being used; color expressions don't support detection of movement direction, next tiles, and so on.
A plain hex string, like "#ff0000", is a valid color expression, but if you want the color expression to vary based on the current tile or somesuch, you'll need
to use one of the arrays. evaluateColor() will convert the color expression into a string that can be used as that color, or gradient, in the HTML/CSS.
The most common color expressions are those that represent single colors. These are five-element arrays: the 0th element is a string saying which color system it's
in, the following four are its dimensions in that system.
The most common 0th element is "@HSLA", for which the 1st element is the hue (0 is red, 60 is yellow, 120 is green, 180 is cyan,
240 is blue, 300 is magenta, 360 is red again), 2nd element is the saturation (100 is fully saturated, 0 is greyscale), 3rd element is the lightness (100 is white,
0 is black, 50 is the non-tinted color), and 4th element is "alpha"/opaqueness (1 is fully opaque, 0 is invisible transparent). For example,
["@HSLA", 200, 90, 60, 1] would be this color.
The other two are "@HSVA" (1st element is hue, 2nd is saturation (100 is pure color, 0 is greyscale), 3rd is value (100 is fully light, 0 is black), 4th is alpha)
and "@RGBA" (1st element is red (0 to 255), 2nd is green (0 to 255), 3rd is blue (0 to 255), 4th is alpha (still 0 to 1)).
The four latter elements need to result in numbers, meaning they have to be either plain numbers or CalcArray expressions that result in numbers.
Next are the gradient types. A color expression beginning with "@linear-gradient" will result in a linear gradient of colors.
Each entry after that should be either a color expression that's a single color, or a number (which places the most recent color at that percent through the gradient).
If there's a number right after the "@linear-gradient" (i.e. before any color entries), it sets the angle of the gradient (0 is bottom-to-top,
90 is left-to-right, 180 is top-to-bottom, 270 is right-to-left, and values between multiples of 90 will be some form of diagonal)
For example, if you want a gradient that goes from left-to-right, starts at red, goes to yellow 20% of the way through and stays yellow until 45% of the way through,
then ends at blue, you'd do ["@linear-gradient", 90, ["@HSLA", 0, 100, 50, 0], 0, ["@HSLA", 60, 100, 50, 0], 20, 45, ["@HSLA", 240, 100, 50, 0], 100],
or some variation of such. (Note that any CalcArray within a gradient will be assumed to be a color, even if it would return a number. To mark a CalcArray within a gradient
as "this will return a number for a gradient position, not a color", put "@CalcArrayNumber" at the start of that gradient entry.)
The other gradient types are "@radial-gradient" (gradient positions are still from 0 to 100, with 0 being the center and 100 being the edge),
"@conic-gradient" (gradient positions are from 0 to 360, 0 is at the top and it goes clockwise from there),
and "@repeating-linear-gradient", "@repeating-radial-gradient", and "@repeating-conic-gradient"
are versions of the previous three where, if the last color isn't at the end of the gradient, instead of just having the last color last until the end, it jumps back to the first color
and repeats the cycle.
"@multi-gradient" results in multiple gradients stacked on top of each other. Each entry after the 0th in a "@multi-gradient"
array should itself be a gradient color expression.
"@rotate" has three elements after the starting string, and what it does is take another color expression and rotate its hue by
some amount around the color wheel (clockwise, so 90 degrees would rotate reds to chartreuses, yellows to sea greens, blues to rose magentas, etc.).
The 1st element is the amount of degrees to rotate by, the 2nd element is a boolean that, if true, also inverts the lightness of the color (lightness becomes 100 - lightness),
and the 3rd argument is the color expression to be rotated. If the color expression is a gradient or multi-gradient, all of the colors in it are rotated.
Tile Display Rules
We've covered most of what CalcArrays do themselves now, so it's time to discuss the places in the 2048 Power Compendium mode they're contained within.
I'll use 2187 as my primary example, though I'll pull from other modes where it's necessary.
First of all, how are tile displays generated? Here's what the TileTypes array looks like in 2187:

Each entry of TileTypes defines one tile display rule. The 0th entry of a display rule is either an array like [1, 2] that would match a tile,
or a CalcArray expression that results in a a boolean. When a tile is looking for what display rule to use, it goes through TileTypes from start to end,
stopping once it hits a rule where either the tile array is the same as the 0th entry of the display rule, or running the 0th entry of the display rule
as a CalcArray on that tile results in true (if the array is of the "match a tile" type, it may still try to run it as a CalcArray, but since
an invalid CalcArray operator just results in the first argument, doing so will end up resulting in a number, and thus not the boolean value true).
In the event every display rule fails, it defaults to the last one.
Once a display rule has been decided, the rest of that rule's entries control the tile's display. The 1st entry is the number that'll be displayed on that tile
(this can actually be any type, or a CalcArray that results in any type. If it's a numeric type, that type's defaultAbbrev operator will be run on it after the
value is calculated), the 2nd entry is the color or gradient of the tile's background (a color expression), and the 3rd entry is the color of the tile's text (a color expression).
Tile backgrounds are allowed to be single colors or gradients or multi-gradients, but gradient text is not supported, so tile colors must be single colors.
Some tile types will have additional entries, as seen in the Ratio-Fill modes:

The 4th entry controls the text's shadow effect. This can be written the way CSS does it directly, or as an array of four elements:
in the latter case, the first two elements (numbers) control the horizontal and vertical offset of the shadow from the text,
the third element (a number) controls the blur strength, and the fourth element (a color) is the color of the shadow.
Of course, any of those elements could be CalcArrays (in the case of the fourth it'd be a color expression instead).
Under normal circumstances, a tile's text size is based on how many characters are in the text - for the most part.
The "text length" of a tile is treated as either 2 or (the amount of characters * 0.7), whichever is higher,
and then larger text lengths mean smaller text sizes (inversely proportional).
The 5th and 6th entries of a display rule let you alter this: use a positive number to mean that exact number,
use a negative number to mean (the amount of characters * abs(that number)), and then the text length will be treated
as whichever of those two is higher. (If one of them is set to 0, it reverts to its default, which is 2 for the 5th entry and -0.7 for the 6th)
Finally, any entries beyond the 6th are addons. There are currently three possible types of addons:
-
Additional text on the tile. An entry that adds additional text is an array whose 0th entry is "Innerscript".
The 1st entry of an Innerscript is the text of that Innerscript. The 2nd entry is a string indicating the position, with
nine possible options: the string takes the form "[vertical position]-[horizontal position]", where the [vertical position]
before the hyphen can be top, bottom, or center, and the [horizontal position] after the hyphen can be left, right, or center.
All modes that currently use Innerscripts have "bottom-center" for their positions. The 3rd and 4th entries control the size in the same
way as the 5th and 6th entry of a display rule. The 5th entry controls the text color (which is the same as the tile's text color if
the entries don't get this far), the 6th entry controls the text shadow. Only up to the 2nd entry is required.
-
Another gradient to put as an image on top of the tile's background color/image. This kind of entry is an array whose 0th entry is "PrimeImage",
named as such because it was going to be used for the 180 and DIVE color schemes before they were made into "special" color schemes.
The 1st entry of a PrimeImage is the background color/gradient to be used, and the 2nd entry is the "mask image", which works
like the CSS mask-image property (see this article for a tutorial on that).
-
If you want to create a list of these that has a variable amount of entries, such as if you need the amount of PrimeImages to depend
on the tile, use an "ExtraEntriesList" array. After the "ExtraEntriesList" at the beginning, the rest of the array is evaluated as
a CalcArray. This CalcArray should return an array of addon arrays (i.e. an array of Innerscript and/or PrimeImage arrays),
and then once that has been evaluated, each of those Innerscripts and PrimeImages are themselves evaluated and added to the tile.
Special Color Schemes
Most modes use color expressions to determine the colors/backgrounds of their tiles, but there's a collection of color schemes that
were too complicated to implement via CalcArrays, and thus had to be directly implemented in JavaScript instead.
These are the "special color schemes". To use a special color scheme for a tile instead of its normal display, have "@ColorScheme"
be the display rule's 2nd entry, then put the name of the special color scheme for the 3rd entry, and the 4th entry should be an array
whose 0th entry is the value (usually a BigInt) to input into the special color scheme, and further entries are "parameters" for that special color scheme.
Here's an example of what this looks like:

And here's a list of the special color schemes:
-
"Wildcard 2048" (1st parameter is a boolean: if it's true then numbers are written as multiple powers of 2, such as 7 becoming
"1 2 4", while if it's false then numbers are written normally)
-
"mod 27" (1st parameter, which is 180 by default, rotates the gradient)
-
"1321" (1st parameter controls how fast powers of 2 make it darker (1 by default), 2nd parameter adds to the starting darkness level
(0 by default). This color scheme was originally a CalcArray color scheme; it was only made a special color scheme to reduce
lag in modes like Pro-Add-Uct.)
-
"180" (1st parameter is the amount of primes tracked before switching to inner tiles, 48 by default)
-
"DIVE" (1st parameter is the amount of primes tracked before switching to inner tiles, 168 by default)
-
"2295"
-
"3069"
-
"Odds-Only 3069"
-
"SQUART" (1st parameter is the amount of primes tracked before switching to inner tiles, 168 by default)
-
"SQUARTSingle" (SQUART's color scheme, but with just one segment instead of two, so really it's moreso DIVE's color scheme but
five-smooth colors get brighter faster. 1st parameter is the amount of primes tracked before switching to inner tiles, 168 by default)
-
"Turatin"
-
"3307"
-
"Bitwise 2048" (1st parameter is the base being used, 2 by default)
-
"SCAPRIM" (1st parameter is the amount of primes tracked before switching to inner tiles, Infinity by default)
-
"1845" (1st parameter is the amount of primes tracked before switching to inner tiles, 1229 by default)
-
"3385" (1st parameter is the amount of primes tracked before switching to inner tiles (168 by default),
2nd parameter is the exponent at which the color goes to the right segment (2 by default))
-
"LOCEF" (1st parameter is the amount of primes tracked before switching to inner tiles, 168 by default)
-
"Three-Tile SQUART" (1st parameter is the amount of primes tracked before switching to inner tiles, 168 by default)
-
"TRIGAT"
-
"Anti-DIVE" (An inverted colors version of the DIVE color scheme.
1st parameter is the amount of primes tracked before switching to inner tiles, 168 by default.
This color scheme is not currently used in any mode, but was added for a mode idea in v2.3 that didn't end up
making it into the game, but its color scheme remains.)
-
"Gaussian DIVE" (0th parameter should be a GaussianBigInt instead of a BigInt.
1st parameter is the amount of Gaussian primes tracked before switching to inner tiles, 1232 by default)
-
"Partial Absorb 180" (0th parameter should be a BigRational instead of a BigInt.
1st parameter is the amount of primes tracked before switching to inner tiles, 27 by default)
-
"RACUTE", "Rational DIVE" (0th parameter should be a BigRational instead of a BigInt.
1st parameter is the amount of primes tracked before switching to inner tiles, 168 by default.
These two are synonyms)
Special color schemes can also be used in PrimeImages. To do so, instead of having the 1st entry of the prime image be the gradient,
have it be an array of the form ["@ColorScheme", whatever the special color scheme is, the value to put into the color scheme, ...color scheme parameters].
Merge Rules
TileTypes is one of the two main places where CalcArrays are used in every mode.
The other one is MergeRules, which is in my opinion the most important part of a mode, since it's where the rules of the mode,
i.e. what tiles can merge, are. Here's 2187 again:

-
The 0th entry of a merge rule is the length of the merge.
-
The 1st entry of a merge rule is a CalcArray that returns a boolean. The merge is considered valid if, when some tiles collide, that CalcArray returns true when run on
the tile furthest backwards in the movement direction (i.e. the one colliding into the rest).
-
The 2nd entry of a merge rule is a boolean: if this boolean is true then the merge will only work if the tiles are in the precise order that the 1st entry would suggest.
If this boolean is false, then the tiles can be in any order; this is implemented via replacing the "@This" and "@Next" strings to effectively rearrange them,
testing all possible permutations. The amount of permutations to test is the factorial of the merge length, so if the merge length is more than 4 (and perhaps even for 4 itself),
I'd advise against using this functionality. Instead, I'd suggest setting the boolean to true, and if you need some way to make the merge reorderable, write your CalcArray to do
so more efficiently.
-
The 3rd entry is the array of output tiles from the merge; this is an array of tiles rather than a single tile because of Partial Absorb modes.
Each entry of this array is a tile, so each entry of those arrays is an element of a tile array, and only arrays inside those arrays will be interpreted as CalcArrays.
-
The 4th entry is how much the score changes by from doing this merge. Note that score is a number, so this will be type-converted into a number after the CalcArray is evaluated.
-
The 5th entry is a list of whether that space is considered "open" and thus able to merge again that turn. This entry is mostly superfluous, as most modes have it default to
"false for spaces that have output tiles, true for spaces left empty", but it's used otherwise in a few cases (Like Garbage 0s and 3,188,646's multiplication tiles).
The default behavior is what occurs if the 5th entry is not present, or is an empty array.
Like with TileTypes, entries earlier in MergeRules are checked first when tiles collide. But an additional precaution has to be taken here:
if, for example, two or three of the same tile can merge, putting the three-tile merge first is necessary, but not sufficient, because the two-tile collision
will occur before the three-tile collision does. This is why @NextNE strings exist, as seen in 1296's MergeRules:

["@NextNE -1 0", "!=", "@This 0"] in the third merge rule is there specifically to disallow the two-tile merge if the three-tile merge is coming up.
Modes like Isotopic 256 have effects that occur to individual tiles at the end of a turn. In many cases, this is done by a merge whose length
(0th entry) is 0. Length-0 merges do not occur during the moving process of a move; instead, they occur once all the tiles have finished moving and merging (but before new random tile(s) spawn),
and they occur to each tile individually.
Merge length 0 is the official way to do "merges" that only alter one tile. Merges with a length of 1 are not officially supported, and I'm not sure what the engine would
do if you tried to include one. I suspect it'd be like a length 0 merge but it can occur in the middle of a move instead of only at the end, but I don't know.
A few merge rules, like those in XXXX, have ten entries instead of six:

When this is the case, that merge rule can take on multiple lengths.
This works by having it start at the given length, then create copies of the rule by incrementing the length, and at each increment it pastes in a new copy of the 1st entry's CalcArray
(the 1st entry now becomes a CalcArray containing all of the copies, separated by "&&"s), but with some of the "@Next" strings having their first index increased on each copy
(in this context an "@This" string acts as an "@Next 0" string and thus also increments).
The 0th entry now instead refers to the minimum merge length that the rule is valid for, the 6th entry is the length that the merge rule as given is, the 7th entry
is a list of how much to increment the first index of the "@Next" strings by (Strings that were "@This" in the original are incremented by the 0th entry of the 7th entry,
strings that were "@Next 1" in the original are incremented by the 1st entry of the 7th entry, strings that were "@Next 2" in the original are incremented by the 2nd entry of the 7th entry,
and so on), the 8th entry is how much to increase the merge length on with each increment, and the 9th entry is either a single number (the maximum allowed merge length) or an array of numbers
(only those merge lengths are allowed).
A merge rule has to have five, six, or ten entries; the 5th entry isn't necessary on its own, but once you're going for a multi-length merge rule you need to have all four of the
multi-length entries. The turning of a multi-length merge rule into multiple copies occurs at the start of the game, so the multi-length merge rule will not remain as a
single merge rule once the game has begun.
It is possible for a merge to have more outputs than inputs. This is called a "Merge Overflow" merge, and in this case there's a few special strings you can use to indicate
how the overflow behaves. These strings go at the start of the 3rd entry of a merge rule, i.e. at the beginning of the array of output tiles.
Here are the merge overflow strings:
-
"@MergeOverflowEmpty": The merge only occurs if there are enough empty spaces directly behind the merging tiles to fit the overflow tiles.
(This is the default behavior if no overflow string is given)
-
"@MergeOverflowSlot": The merge only occurs if there are enough empty spaces behind the merging tiles to fit the overflow tiles,
but those empty spaces don't have to be next to each other; the overflow output tiles can jump over non-empty spaces in their spawn locations.
-
"@MergeOverflowOverwrite": The overflow tiles will fill in the spaces directly behind the merging tiles, even if they have
to replace existing tiles to do so.
-
"@MergeReverseStart": This string reverses the output order of the tiles. If there's no merge overflow then this isn't very useful since you could just
reverse the order of the output tiles in the 3rd entry of the merge rule, but if there is merge overflow, then this string also causes the overflow to go to the tiles ahead of the merging tiles
instead of behind. This string can (and, if you're using it at all, probably should) be placed at the start of an output tiles array that also has one of the other overflow strings;
it doesn't matter which order the two are in. (If you try to put multiple of the other three overflow strings at the start of the same output array, whichever of those three is last
will take priority. Two "@MergeReverseStart"s in the same output tiles array will cancel each other out. But whatever you do with these, make sure they all go before any of the output tiles.)
Tile Spawns
The variable startTileSpawns is used to define the possible spawning tiles. Each element of this array is itself a two-element array representing one possible spawning tile,
where its first element is the tile itself and its second element is the chance of it spawning.
These chances do not have to be out of 100%; it simply means that a tile with a larger chance is more likely to spawn than one with a smaller chance.
Normally the spawning tiles and chances are written as plain arrays and numbers respectively, though you can put CalcArrays into a tile's entries or a spawning chance if you wish.
If you want an entire spawned tile to be evaluated as a CalcArray expression (which you'll need to do if you don't want the result to be an array,
such as if you want to spawn a temporary hole), put "@STCalcArray" at the start of that spawning tile.
If a spawning tile array's first entry is "Box", then the second entry is still the chance, but there are more entries after that.
This is used to denote spawns like those in 3072 or 1535 1536 1537, where there's a "box" containing a select amount of select tiles that refills when it runs through them all,
ensuring a particular long-term distribution of spawning tiles instead of leaving it up to random chance. After the second entry, the next entry is a spawning tile,
then the next entry is how many of that tile are in the box, and repeat.
There's also the start_forcedSpawns array. Each entry of start_forcedSpawns is an array consisting of a CalcArray expression, a string, a boolean or an array of one or two booleans, and one or more tile arrays.
If the CalcArray expression is true this turn, then all of the tiles in this entry will be spawned this turn, either before or after the random spawns depending on the string,
which can be "BeforeSpawns" or "AfterSpawns". This is used by the Temporary Holes modifiers.
If the boolean, or the 0th entry of the boolean array, is true, then if that tile fails to spawn because the board is full, you immediately lose.
If it's a boolean array and it has a 1st entry that's true, then that forced spawn will only occur once, i.e. once it spawns (or fails to spawn because the board is full)
it's removed from the forced spawns array.
startTileSpawns and start_forcedSpawns are what the tile spawns and forced spawns are at the start of a mode.
There are CalcArray operators (more on those later) that can edit the tile spawns and forced spawns, so there are also variables
TileSpawns and forcedSpawns that store the current spawns instead of the starting ones
(but if your goal is to make an injected mode, you should only be working with the starting versions, not the current ones).
Scripts
Some modes have "scripts", CalcArrays that aren't associated with any other object, and are instead evaluated on their own at particular times in the game.
These are primarily used for random goals, but some modes have other uses for them. For example, here's what 1762's scripts entry looks like when its random goals
are in the "Random goals build upon the previous goals." setting:

Each entry of scripts is an array with two elements, which collectively are a "script": the 0th element is the CalcArray to be evaluated,
and the 1st element is a string that indicates when this script should be triggered.
Though the script's CalcArray has to be a full CalcArray, meaning it has to start with a running value and eventually result in something,
the result value of a script isn't used for anything, so scripts are only useful if they modify things outside themselves.
Most of the time, this means modifying the game variables. In the 1762 random goals example, "@GVar 0"
is being used to store the current random goal, "@GVar 1" is storing how many random goals have been reached so far,
and "@GVar 2" is a boolean that's normally false. The first script's job is to set "@GVar 2" to true
when a tile equal to the current goal is merged, and the second script's job is to increase the random goal at the end of the turn, including increasing your goals reached
count, setting "@GVar 2" back to false, and doubling the random goal then increasing it by -1, 0, or 1 at random
(since the tiles reachable from a tile N in 1762 in one merge are 2N-1, 2N, and 2N+1).
The process of evaluating a script is, for the most part, no different than evaluating any other CalcArray.
The new part here is that string indicating when to run the script. Here's the list of such strings:
-
"BeginTurn": The script runs at the start of each turn.
-
"EndTurn": The script runs at the end of each turn. To be specific, it runs after new tile(s) spawn, but before the
win conditions and such are checked.
-
"Merge": The script runs whenever a merge occurs (not including length-0 merges).
If "@var_retain" or one of the other such variable-retaining starting strings is included at the start of the CalcArray,
then the variables of the merge rule are included, and one more variable comes after them, that being an array of the tiles resulting from the merge.
-
"EndMovement": The script runs once all the tiles have finished moving (but before length-0 merges).
-
"EndMovementDirection": The script runs right before the EndMovement scripts;
unlike EndMovement scripts, these can trigger even on automatic moves that don't trigger beginning/end scripts.
-
"EndMovementMoveless", "EndMovementDirectionMoveless":
Same as the above two, but these can trigger even if no movement occurred this turn.
-
"MoveIteration": The script runs after each "space moved", i.e. after every tile that's going to move moves one move in the direction of movement.
-
"TileMove": The script runs after any tile moves.
-
"PossibleEnd": The script runs when the movement of that turn is about to finish; if there are any of these scripts,
the end of the turn is postponed in case tiles can still move after the script (the turn then ends if no tiles move directly afterwards).
-
"PreSpawn": The script runs right before the new random tiles spawn.
-
"PostSpawn": The script runs right after the new random tiles spawn.
If "@var_retain" or one of the other such variable-retaining starting strings is included at the start of the CalcArray,
then one variable is included, that being an array of all the tiles that just spawned.
-
"ZeroMerge": The script runs whenever a length-0 merge occurs.
If "@var_retain" or one of the other such variable-retaining starting strings is included at the start of the CalcArray,
then the variables of the merge rule are included.
-
"PossibleOver": The script runs when it's about to be Game Over: if there are any of these scripts, the Game Over is postponed in case it's not quite game over yet
(but if there are still no moves left, then it's game over for real).
-
"Victory": The script runs upon winning (right before the win screen pops up)
-
"GameOver": The script runs upon losing (right before the Game Over screen pops up)
-
"TrueEndTurn": The script runs at the very end of the turn, after all the win condition stuff is checked (but before Victory or GameOver scripts).
-
"None": The script is not triggered automatically, but can still be called directly in CalcArray expressions
(this is true of any type that aren't the ones listed above, but "None" is the recommended way to denote this).
Stat Boxes
The boxes above the grid that keep track of statistics in the game, such as your score or the Discovered Tiles, are also defined via arrays containing CalcArrays and other entries.
Each entry of the statBoxes array is a single stat box, and for many modes statBoxes is just [["Score", "@Score"]],
meaning the only stat box is the score box.
(wondering where it is in the mode definitions for some modes? It's at the top of loadMode(), set before the individual mode defining code, so if a mode
doesn't do anything else with the statBoxes then it defaults to that, rather than the default being specified in every mode it applies to).
But some modes have more going on with their stat boxes. Here's 2592's:

And here's DIVE's:

When a mode has multiple stat boxes, the ones listed first in statBoxes are the leftmost ones.
For those unfamiliar with JavaScript syntax, the arrays of commas with ... before them are used to mean that an amount of arguments equal to the amount of commas
are set to their defaults. So that means there's a lot of possible elements for stat box definitions! Only the 0th and 1st elements are required, though.
Here's what they all do:
-
The 0th element is the title of the stat box, and the 1st element is the value it displays.
-
The 2nd element is a boolean. If that element is true, this stat box goes below the grid instead of above it.
-
The 3rd element is also a boolean. If that element is true, the stat box clears the space around it, meaning it's the only stat box in its row (other stat boxes will go above or below it).
-
The 4th element controls the display type. Normally the stat box will just display text, but if its 4th element is "Tile" then it will display whatever its value is as if it's a
tile (like how random goals are displayed), and if its 4th element is "TileArray" then it'll display its value as an array of tiles (like DIVE's seeds).
If the 4th element is one of those two special values, then the 5th element needs to be either the name of a special color scheme (which will display the tile(s) in that color scheme),
or "Self" (which will display the tile(s) as tiles from the mode being played). Putting anything other than one of the two special values for the 4th element will use the regular text behavior.
-
If there's a 6th entry, then the stat box will only be visible if that entry evaluates to true.
-
If there's a 7th entry, then when the stat box is clicked, that CalcArray will be evaluated. Like with scripts, nothing is done with its return value,
so this only makes sense if it's going to modifiy something like the game variables. Stat boxes can only be clicked between moves, not during a move.
-
The 8th entry controls the border around the stat box, and it can be a string, a boolean, or an array that's a pair of a number and a single-color color expression.
If it's a boolean, then if it's false there is no border, and if it's true then there is a border, whose color is the mode's text color.
If it's a string, the border property in CSS is set to that string. If it's an array, then the 0th entry controls the size of the border, the 1st entry controls the color of the border.
-
Entries beyond the 8th are not yet used in an existing Compendium mode, but they do exist. The 9th entry controls the color of the box (which is the same as the space between tiles by default),
the 10th entry controls the color of the box's value text (which is white by default), the 11th entry controls the color of the box's title text
(which is the same as the mode's text color by default), and the 12th entry controls the shadow behind the box (which is none by default; this can be set as a string or a four-entry array
in the same manner as the text shadow entry of tile display rules).
With all those entries put together, it's theoretically possible to make a stat box behave as a button that does something when pushed, though no Compendium mode has done this yet -
clickable stat boxes were added mostly for the sake of toggling how Discovered Tiles is displayed.
Other Special Operators
There are some CalcArray operators I didn't mention in the previous parts because they access or modify some of the in-game objects that
were introduced here in Part 4, so here's a list of them:
-
evaluateColor (1 argument): Argument is an array, which is evaluated as a color expression -
basically, this is the CalcArray operator, but evaluating a color expression instead of a CalcArray.
Results in the string that that color expression evaluates to.
-
"@add_score" (2 arguments): Adds the second argument to the score, then results in the first argument (so the running value is unchanged by this operator).
-
"@replace_tile" (4 arguments): Puts a tile on the grid in a particular position, overwriting whatever tile was there before.
The second and third arguments are the coordinates to put the tile at, the fourth argument is the tile itself.
The fourth argument can be any type, so you can use "@Empty" or the like as well. Results in the first argument.
-
"@edit_mvar", "@add_mvar", "@insert_mvar", "@remove_mvar":
Similar to the four gvar operators, but these alter the modifier variables array instead.
-
"@edit_spawn", "@add_spawn", "@insert_spawn", "@remove_spawn":
These four alter the spawning tiles array.
-
"@edit_forced_spawn", "@add_forced_spawn", "@insert_forced_spawn",
"@remove_forced_spawn": ...you can probably guess what these ones do.
-
"@run_script" (2 arguments): Second argument is a number; this operator runs whichever script is in that index of the scripts array.
Results in the first argument.
-
"tileValue" (2 arguments): Each mode has a CalcArray expression associated with it called its "tile value function".
This operator's arguments are the vertical and horizontal coordinates of the tile you want to examine, and this operator results in whatever value the tile value function
gives for that tile. Tile value functions are currently not used for any purpose yet; they are not used to determine what numbers to put on tiles (as we saw earlier,
the TileTypes entries do that), but they've been made to result in the expected values for existing modes (including custom modes).
I added the tile value function in case at some point I want to add a global modifier that requires the values of tiles for some reason.
-
"mergeRuleApplies" (2 arguments): Both arguments are numbers. The first argument is the index of the merge rule in mergeRules to check;
this operator results in a boolean based on whether that merge rule's 1st entry (the condition for merging) would succeed on the current tile...
unless the second argument, which is the "position offset", is nonzero. If the second argument is 1, it looks at the tile that would be "@Next 1" instead, if it's 2 it
looks at the tile that would be "@Next 2" instead, and so on. This is used in modes like Ratio-Fill 3375 as a more advanced version of what "@NextNE" is useful for:
to prevent certain merges from happening if a larger merge which it's a subset of is coming up.
-
"mergeRuleApplies_nonRecursive" (2 arguments): Same as "mergeRuleApplies", except it removes any
"mergeRuleApplies" checks within that array itself, always replacing them with false. Used in custom modes to reduce lag from
"subset merge checks" (as described above) by making them not pointlessly check their own dependent merges recursively.
-
"@ScriptSignal" (2 arguments): Adds the second argument to the "script signals" array, which was set up to do some special things
involving using scripts to affect moves. The script signals array resets whenever a moment in the move process is reached that any type of scripts are run,
but each time such a moment comes up, the script signals from all of the scripts of that type run that time are accumulated.
Script signals only do anything if they're specific strings, and currently there's only one:
-
"@ScriptSignal_MovementOccurred": If this signal is present after the scripts of type
"MoveIteration", "PossibleEnd", "EndMovementMoveless", or "EndMovementDirectionMoveless" are run (those latter two are in there
but not their non-moveless versions since (0, 0) moves don't have move iterations), the usual "if no tiles moved or merged this turn
(unless the move is direction (0, 0), in which case if no tiles have room to spawn), the move is invalid" rule is overridden and the move counts as valid anyway.
This is used by the secret mode with spoiler code [SPMAG] due to its merges actually being scripts rather than typical merge rules.
Part 5: Non-CalcArray Details For Injected Modes
Notable JavaScript Variables
We've covered basically everything relevant to CalcArrays at this point, but knowing how to use CalcArrays doesn't mean much if you don't know
how to put it all together into an injected mode.
I am aware of two main ways to make an injected mode: by editing the Power Compendium's code directly to make the mode and then exporting it as a save code,
or editing an existing save code into a new mode. Let's start with the first one.
If you want to make a mode within the 2048 Power Compendium's code, here are some of the JavaScript variables you'll want to consider (with their types in parentheses):
-
tileNumAmount (number): The amount of elements the tiles have in their arrays.
Yes, this must be constant - every tile in a given mode must have the same amount of elements.
If you want a tile to have a variable amount of elements, make one of its elements an array itself and put the extras there (3069 does this).
-
tileTypes (array of arrays): The list of defined types of tile displays. See the Tile Display Rules section for details.
-
mergeRules (array of arrays): The list of possible merges. See the Merge Rules section for details.
-
startTileSpawns (array of arrays): The list of (random) spawning tiles. See the Tile Spawns section for details.
-
winConditions (array): This array defines the tiles that will be added to the Discovered Winning Tiles when discovered.
Each element of this array is either a tile array (so only that tile counts as a winning tile) or a CalcArray expression (any tile that makes that expression
evaluate to the boolean true will be considered a winning tile), similar to how the tile for Tile Display Rules can be either of those.
-
winRequirement (number or false): The amount of discovered winning tiles required to win the mode.
Can also be set to the boolean false, in which case the mode cannot be won.
-
loseConditions, loseRequirement: Same as the above, but for premature loss instead of victory.
-
postgameAllowed (boolean): True by default. If this is false, then you cannot continue the game after you win.
-
winPriority (boolean): True by default. If this is true, then if you get into a situation where you win and lose on the same
turn, you win. If this is false, then you lose in that situation.
-
mergeResultKnownLevel (0, 1, 2, or 3): v2.1.13 added a system where the game keeps track of what merges have already given known results,
to avoid having to run CalcArrays every time when dealing with the collisions of common tiles, as CalcArrays are much laggier than just running JavaScript where possible.
The strength of this system is controlled by mergeResultKnownLevel:
0 means that knownMergeResults is not used at all, 1 means that knownMergeResults is only used on a per-turn basis (i.e. its learned rules are forgotten at the end of each turn),
2 means that knownMergeResults retains merges whose inputs are all tiles currently on the board but gets rid of the ones that aren't on the board anymore,
and 3 means that knownMergeResults retains all merge results from throughout the game.
This is 2 by default, but if the merge rules change over the course of the game (like in 2592 and 2295),
this must be set to 0 or 1 (if the merge rules can change within a single turn, it must be 0). Length-0 merges are not included in this system.
So far as I am aware, the known merge results system works correctly with Partial Absorb merges, but does not work correctly with Merge Overflow merges
(those with more outputs than inputs), so if you're making a mode with Merge Overflow merges, set mergeResultKnownLevel to 0.
-
knownMergeMaxLength (number): The maximum merge length of the mode. You don't need to set this if mergeResultKnownLevel is 0,
but if you do intend to use known merge results, they need to know how long the merges can get (but you can set knownMergeMaxLength to Infinity if you need to).
Remember to set this - it's easy to forget this one when making an injected mode!
-
knownMergeLookbackDistance (number): How far back into the negative @NextNE tiles the known merge results will examine.
If this is above 1, it also checks @Next tiles in front of the merging tiles (one less of those than it does of the ones behind).
-
tileDisplayKnownLevel (0, 1, 2, or 3): Works similarly to mergeResultKnownLevel, but for storing the displays of tiles instead of the
check results and outputs of merge rules. This one is 3 by default, and currently there's no mode where it has to be anything less,
but in theory you could make a mode where the displays of tiles are dependent on something other than their own elements, so if you do you'll need to lower this.
-
statBoxes (array of arrays): The list of statistic boxes, like the score box. See the Stat Boxes section for details.
-
start_game_vars (array): The game variables at the start of the game.
-
mode_vars (array): A list of variables that are kept track of during the pre-start screen, used for storing
what the settings of mode modifiers are. Injected modes can't have mode modifiers since they just put you right into the game,
so you'll only need this if you're making a mod of the Compendium.
-
scripts (array of pairs): The list of scripts. See the Scripts section for details.
-
There's a few properties to keep track of that are not JavaScript variables, but rather CSS or HTML. Here's how the first mode, 2048, sets these:
 .
.
-
For the CSS properties, "background-image" sets the background image of the pre-start screen of the mode (meaning if you're just making an injected
mode you don't need this), "--background-color" sets the background color or gradient during the game, "--grid-color" is the color of the space between the tiles,
"--tile-color" is the color of empty spaces, and "--text-color" is the color of the rules text and such.
-
For the displayRules function, the first argument is the ID of an HTML element. The function overwrites the innerHTML of that element,
with each successive argument being a pair array representing a child element to add to the one being overwritten, where
the first array element is what kind of HTML element to add and the second array element is the text that HTML element should contain.
When making a mode, only use this on two HTML IDs: "rules_text" for the rules displayed during a game, and "gm_rules_text"
for the rules displayed on the pre-start screen.
-
start_forcedSpawns (array of arrays): The list of forced spawning tiles at the start of the game. See the Tile Spawns section for details.
(P. S. The reason TileSpawns, game_vars, and forcedSpawns have "start" versions is because of the CalcArray modifiers that can modify them,
meaning they need to be reset to their starting versions when the game is restarted.
When making an injected mode, make sure to edit the starting versions, not the in-game versions.)
-
movementParameters (array of three CalcArray expressions): This is
["@VDir", "@HDir", "@SlideAmount"] by default. When a tile is moving, it's actually these, not the
directions and maximum slide amount themselves, it looks at to determine how it moves, which means if you change these expressions,
you can make it so different tiles move in different ways when you move in the same direction.
-
tileValueFunction (CalcArray expression): An expression that should return the "value" of a tile. You don't need to bother with this
unless you intend on using the tileValue operator, or you're making a full-fledged mod of the 2048 Power Compendium rather than just an injected mode.
-
discoveredTilesFilter (CalcArray expression): A CalcArray (missing its first entry) to be run on each potential new discovered tile
before adding it to the discovered tiles list (if it's still undiscovered after doing so). This is used to make it so Discovered Tiles doesn't store duplicates of tiles that are,
depending on the mode and modifiers in question, considered "the same tile" despite their tile arrays being technically different.
There are plenty more variables the Compendium works with, but ones beyond these are generally meant to be used within the "engine", not by the person making the mode.
Save Codes
The 2048 Power Compendium has a few kinds of save codes, but this blog post is documentation on how to make a mode, so I'll only be going over
the main kind of save code, the one that loads either an in-progress game or the start of a mode.
A save code is a text string consisting of a bunch of parts separated by | characters.
The first two parts are in plaintext: the first is "@2048PowCompGame" for in-progress games, "@2048PowCompMode" for new games of modes.
The second is the version number, which updates whenever some new feature is added to CalcArrays or to the save code format - newer versions of the Compendium
can have older save codes loaded, but older versions cannot load newer save codes. So far, every major (first or second version number) update, as well as a few small
(third version number) updates have had the save code version increment; there have been a couple of these were nothing outright new was added to CalcArrays
or the save code format, but the addition of new special color schemes still forced the save code version increment.
The rest of the parts are in base-64 encoding, either of just a plain string or of the object run through JavaScript's "stringify" function -
or, rather, an extended version of stringify that also handles BigInts, BigRationals, and GaussianBigInts via the "@BigInt", "@BigRational", and "@GaussianBigInt"
methods described back in Part 2, as well as using "@Infinity", "@-Infinity", and "@undefined" to store the appropriate values since stringify would otherwise turn them into null.
These save codes include several pieces of data not discussed in the last section, since they also store data related to global modifiers.
Here's the order of the rest of the parts in a mode save code:
-
The width of the grid
-
The height of the grid
-
The layout of the grid at the start of the game, before any tiles have spawned
-
The movement directions
-
The automatic moves
-
movementParameters
-
TileNumAmount
-
TileTypes
-
MergeRules
-
startTileSpawns
-
start_forcedSpawns
-
winConditions
-
winRequirement
-
loseConditions
-
loseRequirements
-
winPriority
-
postgameAllowed
-
statBoxes
-
The "--background-color" CSS property
-
The "--grid-color" CSS property
-
The "--tile-color" CSS property
-
The "--text-color" CSS property
-
The innerHTML of the rules_text HTML element (note: before the base-64, this is encoded via the JavaScript library he, to avoid letting special characters that would mess with
the HTML into the save code)
-
Whether tiles can merge multiple times in the same turn
-
Whether tile spawns can occur anywhere or only on the edge moved away from
-
How many random tiles spawn at the start of the game
-
How many random tiles spawn each time
-
The "spawn conditions", a CalcArray expression. Random tile spawns only occur this turn if the spawn conditions CalcArray evaluates to true.
-
How many of the next spawning tiles are visible
-
start_game_vars
-
start_modifier_vars
-
scripts
-
A boolean that, if true, indicates the grid is hexagonal instead of square
-
Whether or not the tile text is hidden
-
tileDisplayKnownLevel
-
mergeResultKnownLevel
-
knownMergeLookbackDistance
-
knownMergeMaxLength
-
tileValueFunction
-
discoveredTilesFilter
An in-progress game save code includes all of those, and then the following additional pieces:
-
The current state of the grid
-
The score
-
The amount of winning tiles discovered if you haven't already won, -1 if you have already won
-
An array of booleans indicating which movement directions haven't been blacked out currently
-
The current list of spawning tiles (remember, there are CalcArray operators that can modify this)
-
The boxes containing tiles that spawn via spawn boxes
-
The "conveyor" of the upcoming spawning tiles
-
The array of all discovered tiles (This is what "@DiscTiles" accesses)
-
The array of all discovered winning tiles (This is what "@DiscWinning" accesses)
-
The array of all discovered losing tiles (This is what "@DiscLosing" accesses)
-
How many moves have been made so far
-
How many manual moves have been made so far (automatic moves don't increment this)
-
How many merges have been made so far
-
How many moves where merges have occured have been made so far
-
How many merges before the start of the current turn have been made (not sure why I put this in the save codes, since a save code wouldn't be made in the middle of a turn, but oh well)
-
The current game_vars
-
The current modifier_vars
-
A boolean indicating whether the "PossibleOver" scripts, if there are any, have been checked
-
An array of the moves played throughout the game (saved for replay purposes); these moves include the associated spawned tiles as part of them
-
The current move being played (saved for replay purposes)
-
An array storing any non-spawn random events that have occurred this game (saved for replay purposes)
-
An array storing the current "rng index" used for accessing random events during a replay (saved for replay purposes)
-
A list of any tile spawns that didn't come from regular moves this game; currently this is used for automatic moves (saved for replay purposes)
-
The current forcedSpawns










 .
.